Pytorch LayerNorm源码详解

发表于 分类于 本文字数： 3.1k 阅读时长 ≈ 11 分钟

1. LayerNorm使用介绍

pytorch中的函数定义如下：

1
torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, device=None, dtype=None)

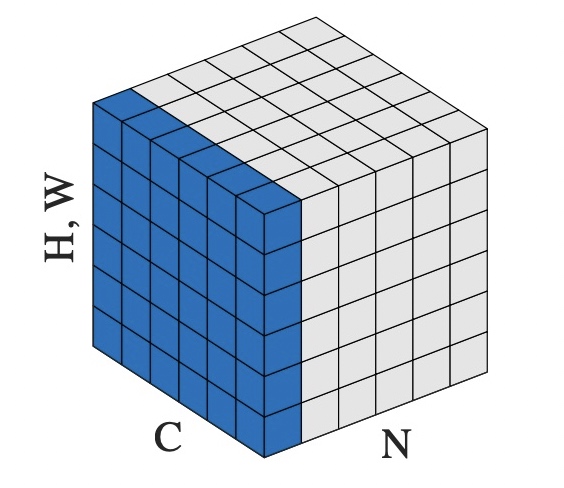
函数参数说明如如下： * normalized_shape: 进行LayerNorm的维度定义，对于一个多维矩阵[N, C, H, W]来说，这里的normalized_shape定义都是要和矩阵最后几个维度保持一致的，这里就是[C, H, W]。对比数学公式，其中的 \(\gamma\) 和 \(\beta\) 的维度都是[C, H, W]，\(x\) 和 \(y\) 的维度都是[N, C, H, W]。 * eps：为了防止计算公式中的分母为0，加上一个极小的数，默认值: 1e-5 * elementwise_affine：设为True的时候，进行elementwise的仿射变换, \(\gamma\) 和 \(\beta\) 才会生效，在训练过程中做为参数会被学习更新，为False的话不生效。\(\gamma\) 所有元素初始为1， \(\beta\) 所有元素初始为0的。\(\gamma\) 在代码实现中对应 \(gamma\), \(\beta\) 在代码实现中对应 \(beta\)。

LayerNorm的数学公式定义如下：

\[\begin{align*} Y &= \frac{X - E[X]}{\sqrt{Var[X] + \epsilon}} * \gamma + \beta \end{align*}\]

pytorch使用示例，给定一个[N, C, H, W]的矩阵，在[C, H, W]维上进行LayerNorm操作：

1
2
3
4
5
6
7
>>> # Image Example
>>> N, C, H, W = 20, 5, 10, 10
>>> input = torch.randn(N, C, H, W)
>>> # Normalize over the last three dimensions (i.e. the channel and spatial dimensions)
>>> # as shown in the image below
>>> layer_norm = nn.LayerNorm([C, H, W])
>>> output = layer_norm(input)

2. LayerNorm反向推导公式

为了方便推导，eps先忽略，输入为一维矩阵。对应LayerNorm的数学公式定义如下, 其中\(x\)是由\([x_1, ...,x_i, ..., x_N]\)组成的一维向量, \(y\)是输出向量，维度跟\(x\)一样; \(E[x]\)是期望，简写为\(\mu\); \(Var[x]\)是方差【\(\frac{1}{N} \sum^N_{i=1}{(x_i-\mu)^2}\)】; 标准差【\(\sqrt{Var[x]}\)】简写为\(\sigma\)。

\[\begin{align*} y &= \frac{x - E[x]}{\sqrt{Var[x]}} * \gamma + \beta \\ &= \frac{x - \mu}{\sigma} * \gamma + \beta \\ &= \hat{x} * \gamma + \beta \\ \\ \mu &= \frac{1}{N}\sum^N_{j=1}{x_j} \\ \\ \sigma &= \left( \frac{1}{N} \sum^N_{j=1}{(x_j-\mu)^2} \right)^{\frac{1}{2}} \\ \\ \hat{x} &= \frac{x-\mu}{\sigma} \\ \\ \end{align*}\]

这里有三个地方需要求梯度(即需要进行求导)，分别是对参数gamma\((\gamma)\)和beta\((\beta)\), 以及输入x的求导, 即\(\frac{\partial{l}}{\partial{\gamma}}\)、\(\frac{\partial{l}}{\partial{\beta}}\)、\(\frac{\partial{l}}{\partial{x}}\)。同时在计算 \(\frac{\partial{l}}{\partial{x}}\) 时会用到 \(\frac{\partial{\mu}}{\partial{x}}\)，\(\frac{\partial{\sigma}}{\partial{x}}\)，\(\frac{\partial{\hat{x}}}{\partial{x}}\)。

\[\begin{align*} \frac{\partial{l}}{\partial{\gamma_i}} &= \frac{\partial{l}}{\partial{y_i}} * \frac{\partial{y_i}}{\partial{\gamma_i}} \\ &= \frac{\partial{l}}{\partial{y_i}} * \frac{x_i - \mu}{\sigma} \\ \\ \frac{\partial{l}}{\partial{\beta_i}} &= \frac{\partial{l}}{\partial{y_i}} * \frac{\partial{y_i}}{\partial{\beta_i}} \\ &= \frac{\partial{l}}{\partial{y_i}} * 1 \\ \\ \frac{\partial{\mu}}{\partial{x_i}} &= \frac{1}{N} \\ \\ \\ \frac{\partial{\sigma}}{\partial{x_i}} &= \frac{1}{2} * \left( \frac{1}{N} \sum^N_{j=1}{(x_j-\mu)^2} \right)^{-\frac{1}{2}} * \frac{\partial{}}{\partial{x_i}} \left( \frac{1}{N} \sum^N_{j=1}{(x_j-\mu)^2} \right) \\ &= \frac{1}{2} * \sigma^{-1} * \frac{\partial{}}{\partial{x_i}} \left( \frac{1}{N} \sum^N_{j=1}{(x_j-\mu)^2} \right) \\ &= \frac{1}{2} * \sigma^{-1} * \frac{1}{N} * 2 * (x_i - \mu) \\ &= \sigma^{-1} * \frac{1}{N} * (x_i - \mu) \\ \\ \frac{\partial{\hat{x}}}{\partial{x_i}} &= \frac{\partial{(x_j - \mu)}}{\partial{x_i}} * \sigma^{-1} + (x_j - \mu) * (-1) * \sigma^{-2} * \frac{\partial{\sigma}}{\partial{x_i}} \\ &= \sigma^{-1} * (\delta_{ij} - \frac{\partial{\mu}}{\partial{x_i}}) + \sigma^{-2} * (x_j - \mu) * (-1) * \frac{\partial{\sigma}}{\partial{x_i}} \\ &= \sigma^{-1} * \delta_{ij} + \sigma^{-1} * (- \frac{1}{N}) + \sigma^{-2} * (x_j - \mu) * (-1) * \frac{\partial{\sigma}}{\partial{x_i}} \\ &= \sigma^{-1} * \delta_{ij} + \sigma^{-1} * (- \frac{1}{N}) + \sigma^{-3} * \frac{1}{N} * (x_j - \mu) * (x_i - \mu) * (-1) \\ &[当i和j相等时，\delta_{ij}=1，否则\delta_{ij}=0] \\ \\ \frac{\partial{l}}{\partial{x_i}} &= \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \frac{\partial{y_j}}{\partial{x_i}} \\ &= \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \frac{\partial{y_j}}{\partial{\hat{x_j}}} * \frac{\partial{\hat{x_j}}}{\partial{x_i}} \\ &= \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * \left[ \sigma^{-1} * \delta_{ij} + \sigma^{-1} * (- \frac{1}{N}) + \sigma^{-3} * \frac{1}{N} * (x_j - \mu) * (x_i - \mu) * (-1) \right] \\ \end{align*}\]

这里 \(\gamma_i/\beta_i\) 与 \(x_i\) 是一一对应的, 所以不用累加；但对于 \(x_i\) 参与了所有 \(y\) 的计算，反向的时候计算梯度也需要对涉及的所有的 \(y_i\) 相关的梯度进行累加。

3. 源码实现

代码仓版本：https://github.com/pytorch/pytorch/tree/v2.0.1

3.1 前向计算

在aten/src/ATen/native/native_functions.yaml中的定义如下： 

1
2
3
4
5
6
7
8
9
- func: native_layer_norm(Tensor input, SymInt[] normalized_shape, Tensor? weight, Tensor? bias, float eps) -> (Tensor, Tensor, Tensor)
  dispatch:
    CPU: layer_norm_cpu
    CUDA: layer_norm_cuda
    MPS: layer_norm_mps
    CompositeExplicitAutograd: math_native_layer_norm
    NestedTensorCPU, NestedTensorCUDA: nested_layer_norm
  autogen: native_layer_norm.out
  tags: core

这里以layer_norm_cpu的实现为例，layer_norm_cpu定义在aten/src/ATen/native/layer_norm.cpp中。

在layer_norm_cpu的前向函数中，会根据input和normalized_shape进行shape的转换计算，从多维矩阵转为\(M \times N\)的二维矩阵，比如input的shape是[2, 3, 4, 5]，normalized_shape是[4, 5], 那么M=2*3=6, N=4*5=20；同时还会进行weight(对应\(gamma\))和bias(对应\(beta\))矩阵的初始化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
std::tuple<Tensor, Tensor, Tensor> layer_norm_cpu(
    const Tensor& input,
    IntArrayRef normalized_shape, const c10::optional<Tensor>& weight_opt /* optional */, const c10::optional<Tensor>& bias_opt /* optional */,
    double eps) {
  // weight和bias初始化
  c10::MaybeOwned<Tensor> weight_maybe_owned = at::borrow_from_optional_tensor(weight_opt);
  const Tensor& weight = *weight_maybe_owned;
  c10::MaybeOwned<Tensor> bias_maybe_owned = at::borrow_from_optional_tensor(bias_opt);
  const Tensor& bias = *bias_maybe_owned;

  // 计算M和N
  auto M_N = _check_layer_norm_inputs(input, normalized_shape, weight, bias);
  auto M = M_N.first;
  auto N = M_N.second;
  auto X = input.expect_contiguous();
  auto gamma = weight.expect_contiguous();
  auto beta = bias.expect_contiguous();

  // 初始化mean/rstd，维度是M个，每N个input的元素会计算一个mean和rstd
  Tensor mean = at::empty({M}, X->options().dtype(dtype));
  Tensor rstd = at::empty({M}, X->options().dtype(dtype));

  // layer_norm_with_mean_rstd_out中会调用前向kernel(LayerNormKernel)
  layer_norm_with_mean_rstd_out(Y, mean, rstd, *X, normalized_shape, *gamma, *beta, eps, M, N);
  return std::make_tuple(std::move(Y), std::move(mean), std::move(rstd));
}

LayerNormKernel定义在aten/src/ATen/native/cpu/layer_norm_kernel.cpp中，实际的实现是LayerNormKernelImplInternal, 定义如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
template <typename T, typename T_ACC>
void LayerNormKernelImplInternal(
    const Tensor& X,
    const Tensor& gamma,
    const Tensor& beta,
    int64_t M,
    int64_t N,
    T_ACC eps,
    Tensor* Y,
    Tensor* mean,
    Tensor* rstd) {
    ...
}

在LayerNormKernelImplInternal首先了解at::parallel_for函数的使用，它的基本作用是对输入先进行分块，然后通过多线程进行并行处理，如下函数的定义是对[0, M]分成多段，分别调用匿名函数。

1
at::parallel_for(0, M, 1, [&](int64_t start, int64_t end) {...})

回顾下前向计算过程：

\[\begin{align*} y &= \frac{x - E[x]}{\sqrt{Var[x]+eps}} * \gamma + \beta \\ &= \frac{x - \mu}{\sigma} * \gamma + \beta \\ &= (\frac{x}{\sigma} + \frac{- \mu}{\sigma}) * \gamma + \beta \\ \end{align*}\]

匿名函数逻辑中，对于 M * N的矩阵，每次处理N个元素进行LayerNorm操作。mean对应\(\mu\), rstd_val和scale对应\(\frac{1}{\sigma}\), bias对应\(\frac{-\mu}{\sigma}\), 因此, \(y=(x * scale + bias) * gamma + beta\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
  for (const auto i : c10::irange(start, end)) {
    const T* X_ptr = X_data + i * N;
    T* Y_ptr = Y_data + i * N;
    T mean_val;
    T rstd_val;
    // 1. 计算mean_val和rstd_val
    std::tie(mean_val, rstd_val) = RowwiseMoments(X_ptr, N);
    rstd_val = T(1) / std::sqrt(rstd_val + eps);

    const T scale = rstd_val;
    const T bias = -rstd_val * mean_val;
    if (gamma_null || beta_null) {
      for (const auto j : c10::irange(N)) {
        const T gamma_v = gamma_null ? T(1) : gamma_data[j];
        const T beta_v = beta_null ? T(0) : beta_data[j];
        Y_ptr[j] = (X_ptr[j] * scale + bias) * gamma_v + beta_v;
      }
    } else {
      // 2. 计算layer norm的前向公式
      vec::map3<T>(
          [scale, bias](Vec x, Vec gamma, Vec beta) {
            return (x * Vec(scale) + Vec(bias)) * gamma + beta;
          },
          Y_ptr,
          X_ptr,
          gamma_data,
          beta_data,
          N);
    }
    if (!mean_null) {
      mean_data[i] = mean_val;
    }
    if (!rstd_null) {
      rstd_data[i] = rstd_val;
    }
  }
}

3.2 反向计算

对于多维矩阵求反向，可以看成是M个大小为N的向量，以一个5维向量为例，向量维度为\([M_1, M_2, C, H, W]\)，layer_norm的维度是\([C, H, W]\)，对应的\(M=M_1*M_2\), \(N=C*H*W\)

在aten/src/ATen/native/native_functions.yaml中的定义如下： 

1
2
3
4
5
6
7
- func: native_layer_norm_backward(Tensor grad_out, Tensor input, SymInt[] normalized_shape, Tensor mean, Tensor rstd, Tensor? weight, Tensor? bias, bool[3] output_mask) -> (Tensor, Tensor, Tensor)
  dispatch:
    CPU: layer_norm_backward_cpu
    CUDA: layer_norm_backward_cuda
    MPS: layer_norm_backward_mps
  autogen: native_layer_norm_backward.out
  tags: core

这里以layer_norm_backward_cpu的实现为例，layer_norm_backward_cpu定义在aten/src/ATen/native/layer_norm.cpp中。跟layer_norm_cpu类似，在backward中初始化相关tensor，和进行kernel的调用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
std::tuple<Tensor, Tensor, Tensor> layer_norm_backward_cpu(
    const Tensor& dY,
    const Tensor& input,
    IntArrayRef normalized_shape,
    const Tensor& mean,
    const Tensor& rstd,
    const c10::optional<Tensor>& weight_opt /* optional */,
    const c10::optional<Tensor>& bias_opt /* optional */,
    std::array<bool, 3> grad_input_mask) {
  ......
  if (M > 0) {
    LayerNormBackwardKernel(
        kCPU, dY, *X, mean, rstd, *gamma, M, N, &dX, &dgamma, &dbeta);
  }
  return std::make_tuple(std::move(dX), std::move(dgamma), std::move(dbeta));
}

为了方便和后续pytorch源码实现中对应，对上面推导公式的最后结果中做下相应的展开，展开如下： \[\begin{align*} \frac{\partial{l}}{\partial{x_i}} &= \sigma^{-1} * \frac{\partial{l}}{\partial{y_i}} * \gamma_i + (-1) * \sigma^{-1} * \frac{1}{N} * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j + \sigma^{-3} * \frac{1}{N} * (\mu - x_i) * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * (x_j - \mu) \\ &= \sigma^{-1} * \frac{\partial{l}}{\partial{y_i}} * \gamma_i + (-1) * \sigma^{-1} * \frac{1}{N} * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j + \sigma^{-3} * \frac{1}{N} * \mu * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * (x_j - \mu) + \sigma^{-3} * \frac{1}{N} * (- x_i) * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * (x_j - \mu) \\ &= \sigma^{-1} * \frac{\partial{l}}{\partial{y_i}} * \gamma_i + (-1) * \sigma^{-1} * \frac{1}{N} * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j + \sigma^{-3} * \frac{1}{N} * (-\mu) * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * (\mu - x_j) + \sigma^{-3} * \frac{1}{N} * (x_i) * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * (\mu - x_j) \\ &= \sigma^{-1} * \frac{\partial{l}}{\partial{y_i}} * \gamma_i + (-1) * \sigma^{-1} * \frac{1}{N} * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j + \sigma^{-3} * \frac{1}{N} * (-\mu) * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * (\mu - x_j) + \sigma^{-3} * \frac{1}{N} * x_i * \left[ \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * \mu - \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * x_j \right] \\ &= \gamma_i * \frac{\partial{l}}{\partial{y_i}} * \sigma^{-1} + \left[ -\sigma^{-3} * \frac{1}{N} * \mu * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * (\mu - x_j) - \sigma^{-1} * \frac{1}{N} * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j \right] + x_i * \left[ \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * \mu - \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * x_j \right] * \sigma^{-3} * \frac{1}{N} \\ \end{align*}\]

kernel的实现在是aten/src/ATen/native/cpu/layer_norm_kernel.cpp文件的LayerNormBackwardKernelImplInternal函数中，实现分为两个阶段：

  1. 初始化一个shape大小为{2, max_threads, N}的buffer矩阵，对应其中的buffer[0]用于dgamma_buffer, buffer[1]用于dbeta_buffer。多线程分别计算dY和X。
  2. 对dgamma/dbeta的值进行累加操作，复用X[i]和dY[i]

对于代码实现是通过两层嵌套进行的，对于第一步来说，最外面是对 \(M*N\) 的矩阵按行进行多线程并行，每个线程处理 \(m_i*N\) 个元素；第二步是按N列进行元素的累加。layer_norm_backward_frame函数中包含了主要的计算逻辑, 后面进一步分析。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
template <typename T>
void LayerNormBackwardKernelImplInternal(
    const Tensor& dY,
    const Tensor& X,
    const Tensor& mean,
    const Tensor& rstd,
    const Tensor& gamma,
    int64_t M,
    int64_t N,
    Tensor* dX,
    Tensor* dgamma,
    Tensor* dbeta) {
  ......
  // 第一步：计算dgamma/dbeta and dX
  at::parallel_for(0, M, 1, [&](int64_t start, int64_t end) {
    int tid = at::get_thread_num();
    TORCH_CHECK(
        tid < num_threads,
        "expect thread id smaller than ",
        num_threads,
        ", got thread id ",
        tid);
    T* dgamma_buffer_ptr = dgamma_null ? nullptr : buffer_data + tid * N;
    T* dbeta_buffer_ptr =
        dbeta_null ? nullptr : buffer_data + num_threads * N + tid * N;
    for (const auto i : c10::irange(start, end)) {
      layer_norm_backward_frame<T, T2, T_ACC>(dY_data, X_data, mean_data, rstd_data, gamma_data, dX_data, dgamma_buffer_ptr, dbeta_buffer_ptr, scale, gamma_null, dX_null, dgamma_null, dbeta_null, N, i);
    }
  });

  // 第二步：计算dgamma/dbeta的累加
  if (buffer_data != nullptr) {
    parallel_for(0, N, 1, [&](int64_t start, int64_t end) {
      for (const auto j : c10::irange(start, end)) {
        T_ACC dgamma_v = T_ACC(0);
        T_ACC dbeta_v = T_ACC(0);
        for (const auto i : c10::irange(num_threads)) {
          dgamma_v += buffer_data[i * N + j];
          dbeta_v += buffer_data[num_threads * N + i * N + j];
        }
        if (!dgamma_null) {
          // NOLINTNEXTLINE(clang-analyzer-core.NullDereference)
          dgamma_data[j] = dgamma_v;
        }
        if (!dbeta_null) {
          // NOLINTNEXTLINE(clang-analyzer-core.NullDereference)
          dbeta_data[j] = dbeta_v;
        }
      }
    });
  }
  ......
}

layer_norm_backward_frame函数中计算dgamma的逻辑如下，对应公式：\(\frac{\partial{l}}{\partial{\gamma_i}} = \frac{\partial{l}}{\partial{y_i}} * \frac{x_i - \mu}{\sigma}\), 其中 \(a=\frac{1}{\sigma}\), \(b=\frac{-\mu}{\sigma}=-a*\mu\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
if (!dgamma_null) {
  const T_ACC a = rstd_data[i];
  const T_ACC b = -a * mean_data[i];
  // Scalar math:
  // for (const auto j : c10::irange(N)) {
  //   dgamma_data[j] += dY_ptr[j] * (a * X_ptr[j] + b);
  // }
  vec::map3<T>(
      [a, b](Vec dgamma, Vec dy, Vec x) {
        return dgamma + dy * (Vec(a) * x + Vec(b));
      },
      dgamma_buffer_ptr,
      dgamma_buffer_ptr,
      dY_ptr,
      X_ptr,
      N);
}

layer_norm_backward_frame函数中计算dbeta的逻辑如下，对应公式：\(\frac{\partial{l}}{\partial{\beta_i}}= \frac{\partial{l}}{\partial{y_i}}\)。

1
2
3
4
5
6
7
8
9
10
11
12
if (!dbeta_null) {
  // Scalar math:
  // for (const auto j : c10::irange(N)) {
  //   dbeta_data[j] += dY_ptr[j];
  // }
  vec::map2<T>(
      [](Vec dbeta, Vec dy) { return dbeta + dy; },
      dbeta_buffer_ptr,
      dbeta_buffer_ptr,
      dY_ptr,
      N);
}

layer_norm_backward_frame函数中计算dx的逻辑如下，对应公式:

\[\begin{align*} \frac{\partial{l}}{\partial{x_i}} &= \gamma_i * \frac{\partial{l}}{\partial{y_i}} * \sigma^{-1} + \left[ -\sigma^{-3} * \frac{1}{N} * \mu * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * (\mu - x_j) - \sigma^{-1} * \frac{1}{N} * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j \right] + x_i * \left[ \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * \mu - \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * x_j \right] * \sigma^{-3} * \frac{1}{N} \\ \end{align*}\]

layer_norm_backward_frame函数核心代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
  if (gamma_null) {
    ......
  } else {
    ds = vec::map3_reduce_all<T>(
        [](Vec x, Vec y, Vec z) { return x * y * z; },
        [](Vec x, Vec y) { return x + y; },
        dY_ptr,
        X_ptr,
        gamma_data,
        N);
    db = vec::map2_reduce_all<T>(
        [](Vec x, Vec y) { return x * y; },
        [](Vec x, Vec y) { return x + y; },
        dY_ptr,
        gamma_data,
        N);
  }
  const T_ACC a = rstd_data[i];
  const T_ACC b = (db * mean_data[i] - ds) * a * a * a * scale;
  const T_ACC c = -b * mean_data[i] - db * a * scale;
  if (gamma_null) {
    ......
  } else {
    vec::map3<T>(
        [a, b, c](Vec dy, Vec gamma, Vec x) {
          return Vec(a) * dy * gamma + Vec(b) * x + Vec(c);
        },
        dX_ptr,
        dY_ptr,
        gamma_data,
        X_ptr,
        N);
  }
}

代码中变量与公式对应关系如下： * ds对应\(\sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * x_j\) * db对应\(\sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j\) * a对应\(\sigma^{-1}\) * scale对应\(\frac{1}{N}\) * b对应\(\left[ \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * \mu - \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * x_j \right] * \sigma^{-3} * \frac{1}{N} = (db * \mu - ds) * a * a * a * scale\) * c对应\(\left[ -\sigma^{-3} * \frac{1}{N} * \mu * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j * (\mu - x_j) - \sigma^{-1} * \frac{1}{N} * \sum_{j=1}^N \frac{\partial{l}}{\partial{y_j}} * \gamma_j \right]=-b * \mu - db * a * scale\) * 最终结果：dx = Vec(a) * dy * gamma + Vec(b) * x + Vec(c)

4. 参考资料