详解MegatronLM序列模型并行训练(Sequence Parallel)

发表于 分类于 本文字数： 2.3k 阅读时长 ≈ 8 分钟

1. 背景介绍

MegatronLM的第三篇论文【Reducing Activation Recomputation in Large Transformer Models】是2022年出的。在大模型训练过程中显存占用过大往往成为瓶颈，一般会通过recomputation重计算的方式降低显存占用，但会带来额外的计算代价。这篇论文提出了两种方法，分别是sequece parallel和selective activation recomputation，这两种方法和Tensor并行是可以相结合的，可以有效减少不必要的计算量。

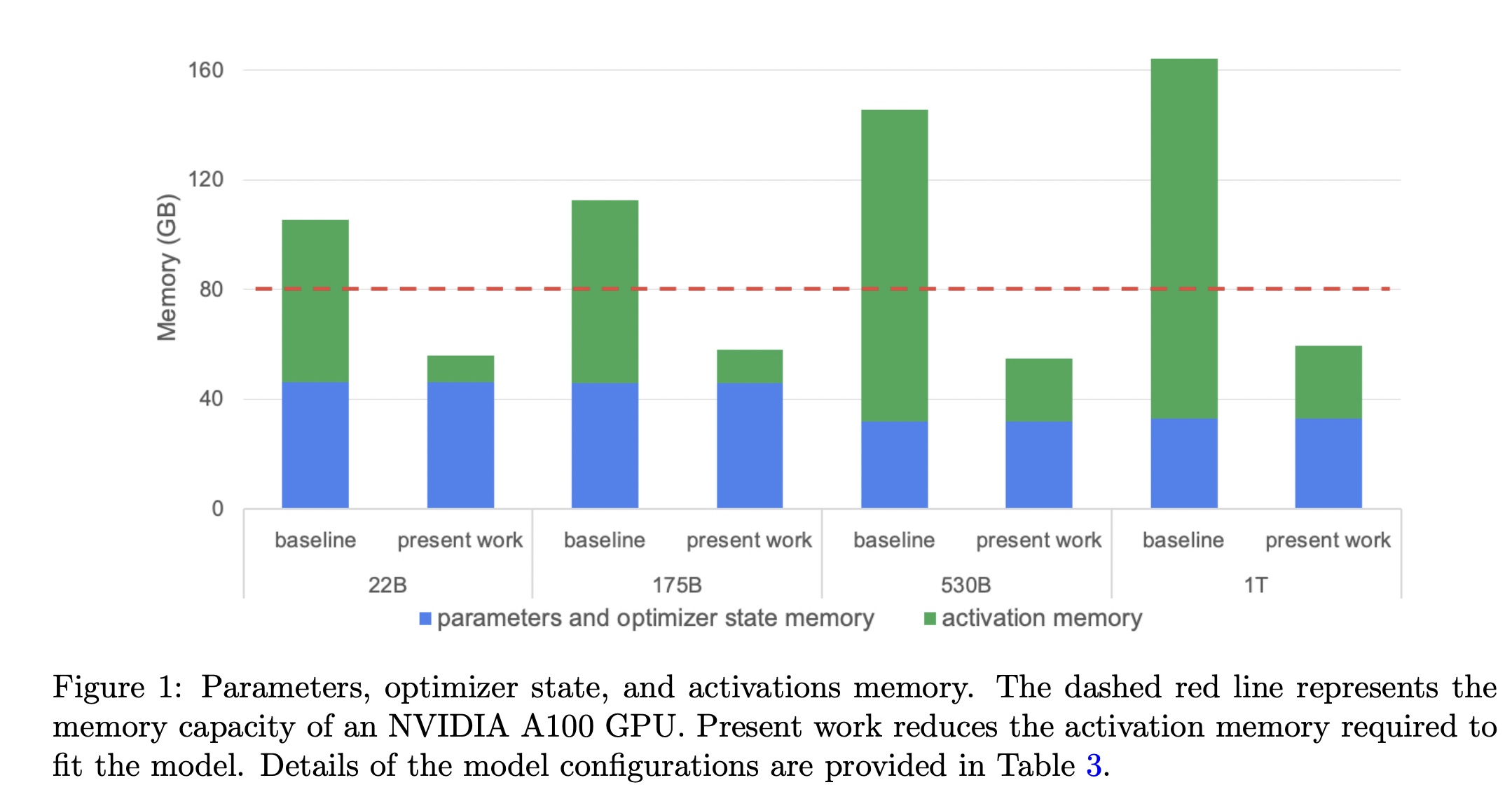
下图中绿色部分表示不同模型中需要用于保存activation需要的显存大小，蓝色部分表示不同模型中需要用于保存parameter和optimizer state需要的显存大小。红色线表示A100的显存大小80G。

2. Pipeline Parallel详细介绍

2.1 估算Transformer Activation Memory大小

以Transformer结构为例估算Activation Memory大小，这里的Activation定义是指前向和反向梯度计算中创建的所有tensor。按这个定义来说，计算不包含模型参数大小和优化器中状态大小，但是包含dropout op用到的mask tensor。

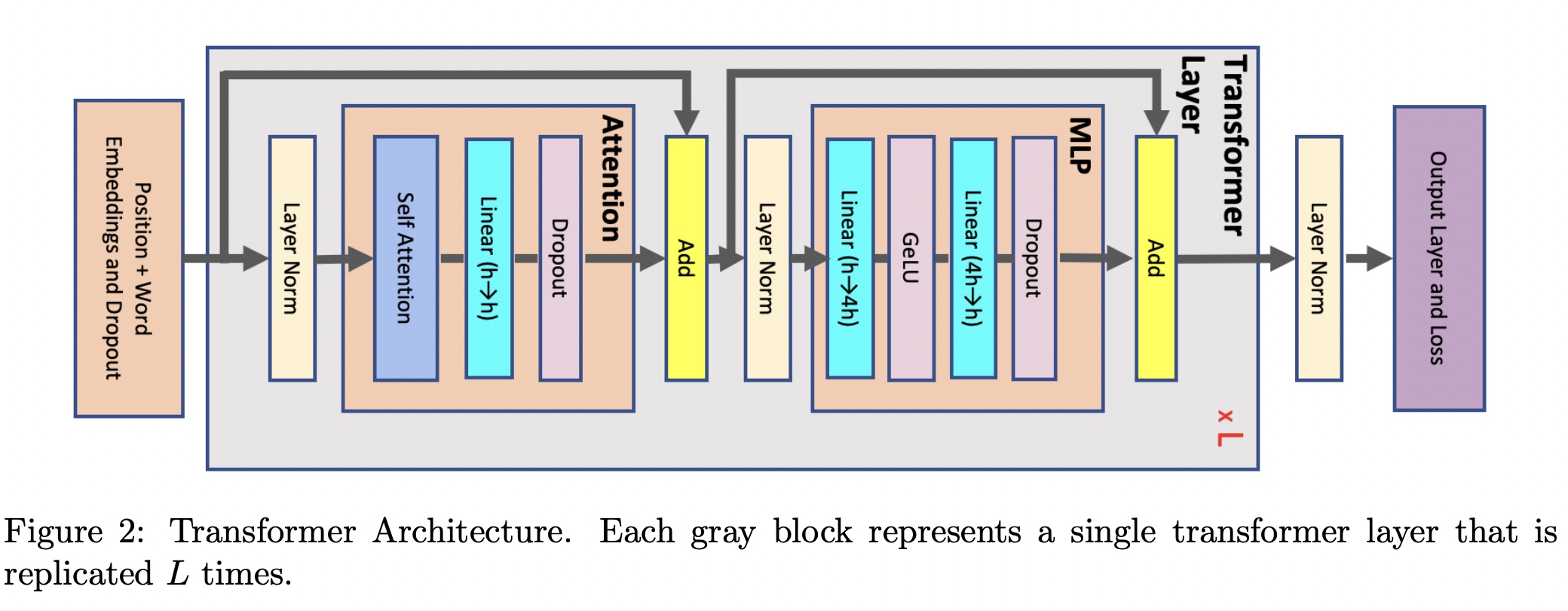
一个Transformer块中由一个Attention块和一个MLP块组成，中间通过两个LayerNorm层进行连接。在Transformer中用到的参数表示如下：

Attention模块的计算公式如下：

\[\begin{gather*} Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V \end{gather*}\]

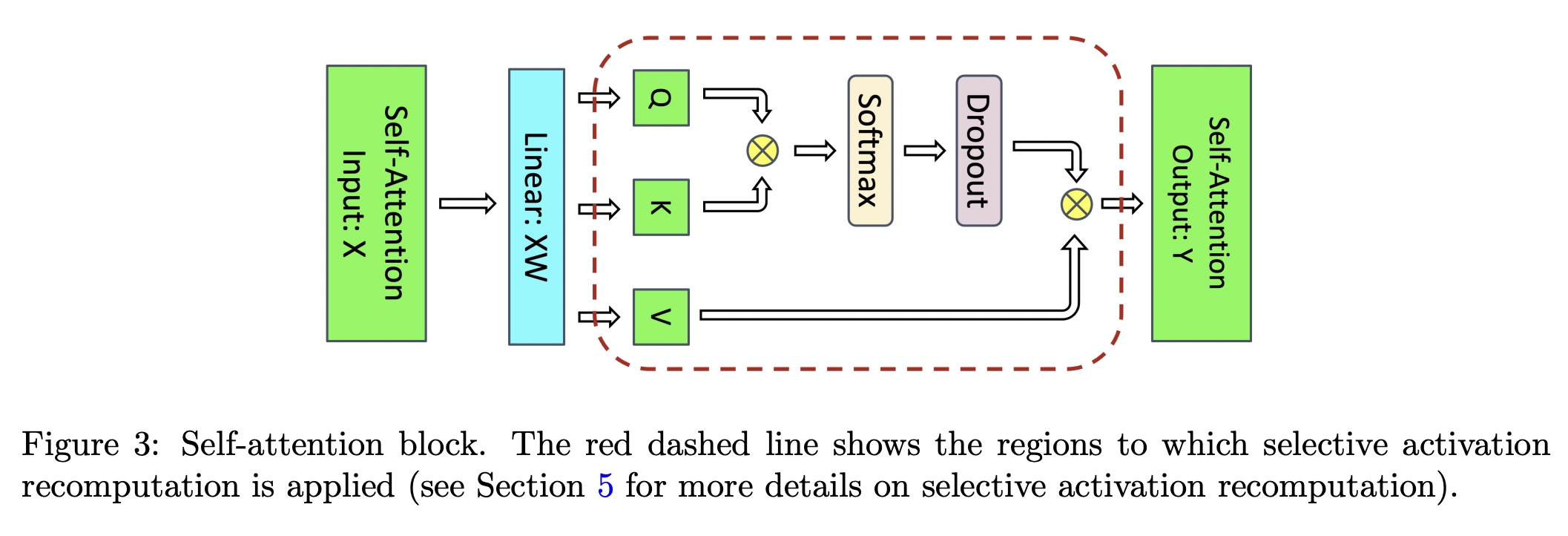
对于Attention块来说，输入的element个数为sbh个，每个element以16-bit的浮点数(也就是2 bytes)来进行存储的话，对应输入的element大小为2sbh bytes，后续计算默认都是按bytes为单位进行计算。

Attention块中包含一个self-attention块、一个linear线性映射层和attention dropout层。对于linear线性映射层来说需要保存输入的Activation大小为2sbh, 对于attention dropout层需要mask的大小为sbh(对于一个元素的mask只用1个bytes即可)，对于self-attention块的Activation Memory的计算有以下几块： * \(Query(Q), Key(K), Value (V)\)矩阵相乘：输入input是共享的，元素个数为sbh个，总大小是 2sbh bytes。 * \(QK^T\) 矩阵相乘：需要分别创建保存 \(Q\) 和 \(K\) 的矩阵，每个矩阵元素总大小为 2sbh bytes, 总共大小为 4sbh bytes。如下图以b=1, s=2, h=6为例，输入\(X\)元素个数为1 * s * h = 12个，计算完后\(Q\) 和 \(K\) 的矩阵中元素个数各有 1 * s * h = 12个，总元素大小为2 * 2 * b * s * h = 48 bytes。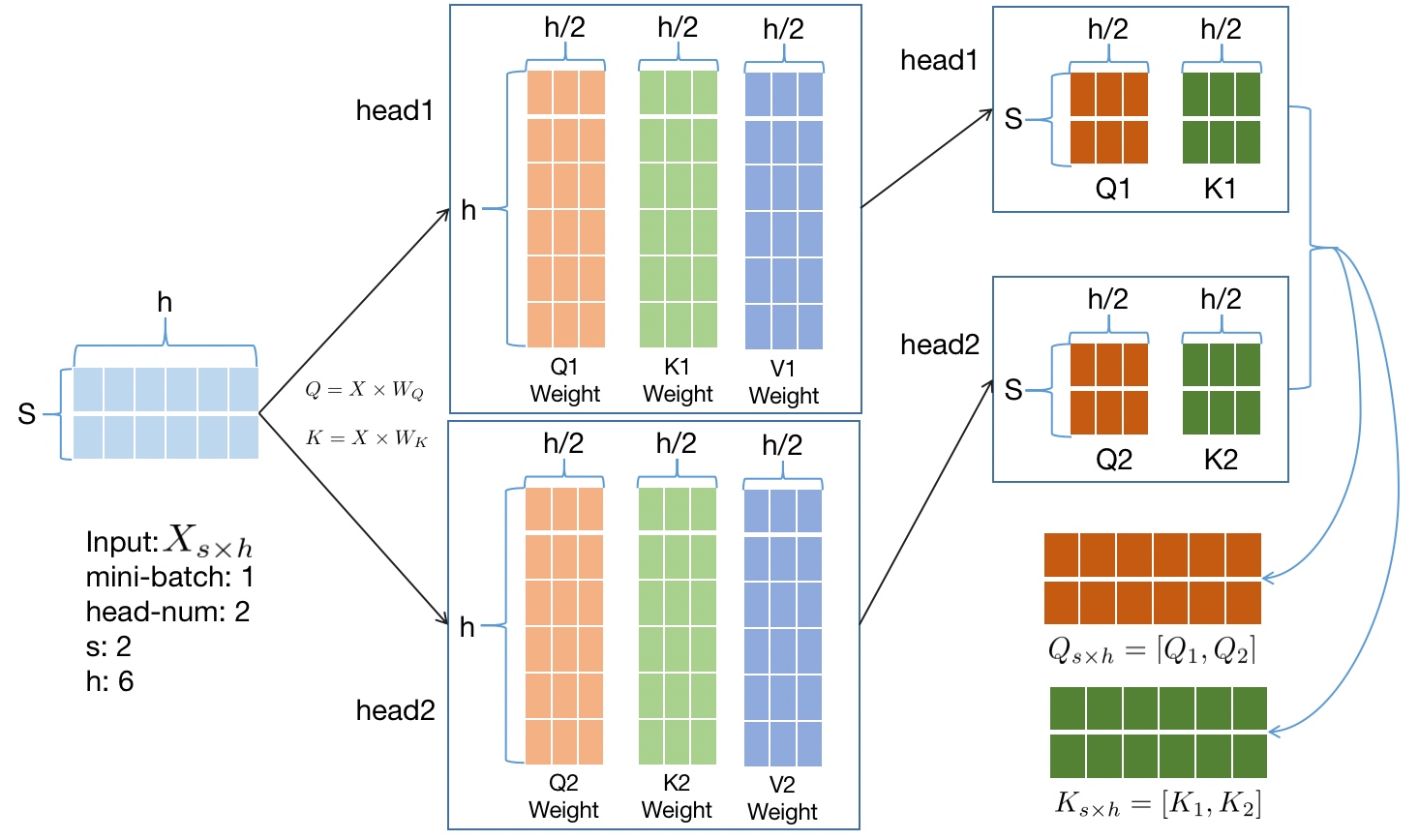

  • softmax的输出总的元素大小为\(2as^2b\) bytes, 分别计算每个Head头的\(Q_n \times K_n\) 的乘积。计算公式如下, 图中计算以b=1, s=2, h=6, a=2为例：

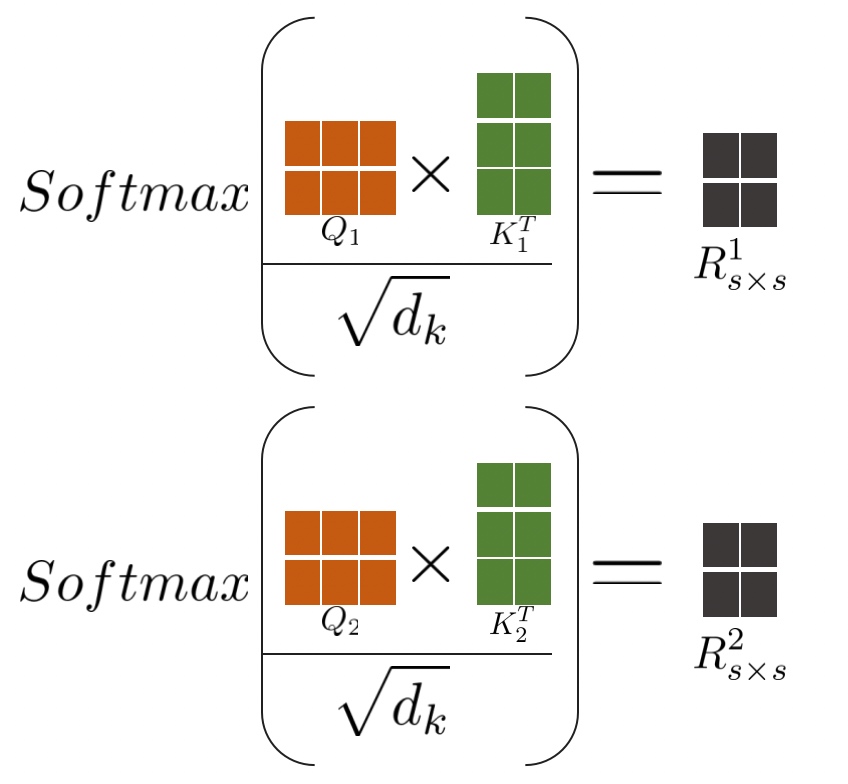
  • 在softmax后还有dropout的mask层大小，mask矩阵的大小与softmax的输出一样，元素个数都是 \(as^2b\) 个，但mask单个元素的大小只用1 bytes即可，总的大小为 \(as^2b\) bytes
  • softmax的输出也会用于反向的计算，需要缓存下来，对应大小也是 \(2as^2b\)
  • \(V\) 矩阵的大小之前没有统计，和 \(Q\)、\(K\)矩阵一样，大小也是2sbh bytes

综上，Attention Block总的大小为 11sbh + 5as^2b bytes。

MLP的Activation大小计算：MLP中有两层线性layer，分别存储输入矩阵大小为 \(2sbh\) bytes和 \(8sbh\) bytes；GeLU的反向也需要对输入进行缓存，大小为 \(8sbh\) bytes; dropout层需要 sbh bytes; 总大小为 19sbh。

LayerNorm的Activation大小计算：每个LayerNorm层的输入需要 \(2sbh\) 大小，有两个LayerNorm层，总大小为 4sbh bytes.

最终transformer网络中一层(含Attention/MLP/LayerNorm)的Activation总的大小为：

\[\begin{gather} ActivationMemoryPerLayer = sbh \left( 34 + 5 \frac{as}{h} \right) \end{gather}\]

注意: 这里公式(1)计算的Activation总和是在没有应用模型并行策略的前提下进行的。

2.2 Tensor Parallel的Activation Memory计算

如下图，在Tensor模型并行中只在Attention和MLP两个地方进行了并行计算，对于Attention(Q/K/V)和MLP(Linear Layer)的输入并没有并行操作。图中 \(f\) 和 \(\overline{f}\) 互为共轭(conjugate)，\(f\) 在前向时不做操作，反向时执行all-reduce; \(\overline{f}\) 在前向时执行all-reduce, 反向时不做操作。

参虑上Tensor并行的话(Tensor并行度为 \(t\))，并行部分有MLP的Linear部分(\(18sbh\) bytes)和Attention的QKV部分(\(6sbh\) bytes)， ActivationMemoryPerLayer相比公式(1)中的值降为： \[\begin{gather} ActivationMemoryPerLayer = sbh \left( 10 + \frac{24}{t} + 5 \frac{as}{h} \right) \end{gather}\]

2.2 Sequence Parallel

在Tensor模型并行基础上提出了Sequence Parallel，对于非Tensor模型并行的部分在sequence维度都是相互独立的，所以可以在sequence维度上进行拆分(即sequence parallel)。拆分后如下图，\(f\) 和 \(\overline{f}\) 替换为 \(g\) 和 \(\overline{g}\)， \(g\) 和 \(\overline{g}\) 也是共轭的，\(g\) 在前向是all-gather通信，反向是reduce-scatter通信；\(\overline{g}\)在前向是reduce-scatter, 反向是all-gather通信。

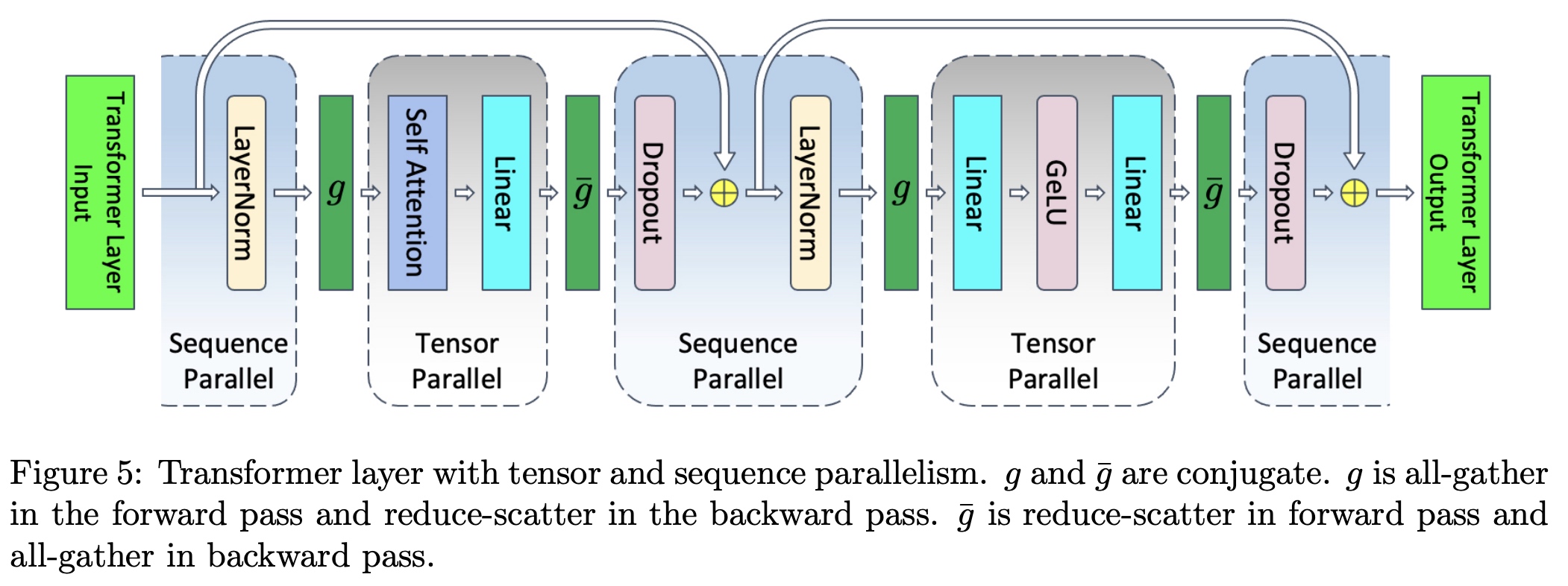
接下来以MLP为例，详细说明拆分步骤。MLP层由两个Linear层组成，对应的计算公式如下, 其中 \(X\) 的大小为 \(s \times b \times h\) ; \(A\) 和 \(B\) 是Linear的权重weight矩阵，大小为 \(h \times 4h\) 和 \(4h \times h\)。

\[\begin{gather*} \begin{aligned} Y &= LayerNorm(X) \\ Z &= GeLU(YA) \\ W &= ZB \\ V &= Dropout(W) \\ \end{aligned} \end{gather*}\]

如下图，切分时说明如下： 1. 对 \(X\) 按sequence维度切分，\(X = \left[ X^s_1, X^s_2 \right]\)，LayerNorm的结果 \(Y = \left[ Y^s_1, Y^s_2 \right]\)； 2. 由于接下来的GeLU不是线性的，所以要进行all-gather操作，计算 \(Z = GeLU(YA)\)； 3. 对 \(A\) 进行列切分的tensor并行，得到结果 \(YA^c_1\) 和 \(YA^c_2\) 4. 对 \(B\) 进行行切分的tensor并行，得到结果 \(Z^h_1 B^r_1\) 和 \(Z^h_2 B^r_2\) 5. 得到 \(W_1\) 和 \(W_2\) 后进行累加操作(reduce-scatter)

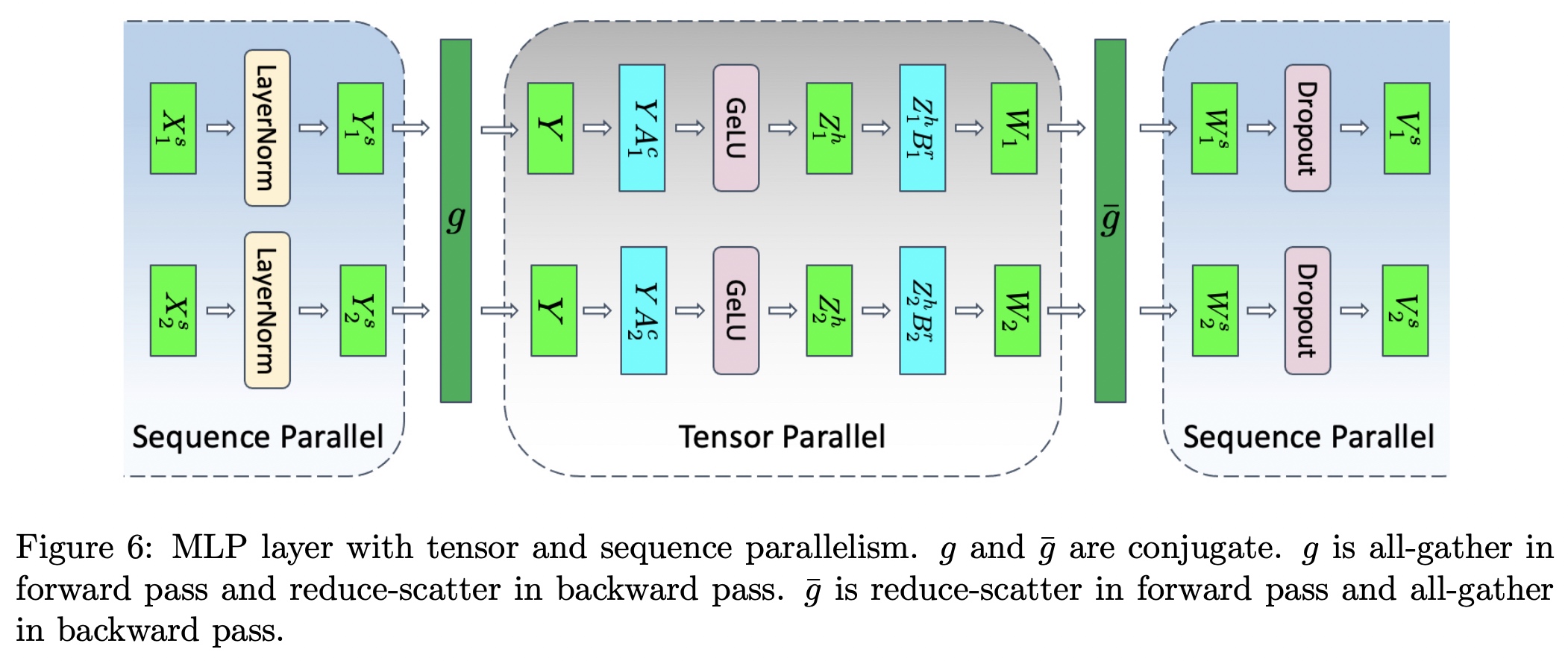
对应的计算公式如下：

\[\begin{gather} \begin{aligned} \left[ Y^s_1, Y^s_2 \right] &= LayerNorm([X^s_1, X^s_2]) \\ Y &= g(Y^s_1, Y^s_2) \\ \left[ Z^h_1, Z^h_2 \right] &= [GeLU(YA^c_1), GeLU(YA^c_2)] \\ W_1 &= Z^h_1 B^r_1 \\ W_2 &= Z^h_2 B^r_2 \\ \left[ W^s_1, W^s_2 \right] &= \overline{g}(W_1, W_2) \\ \left[ V^s_1, V^s_2 \right] &= [Dropout(W^s_1), Dropout(W^s_2)] \\ \end{aligned} \end{gather}\]

Tensor并行在一次前向和后向总共有4次的all-reduce操作，在Sequence并行一次前向和后向总共有4次all-gather和4次reduce-scatter操作。ring all-reduce 执行过程中有两步，先是一个reduce-scatter然后跟着一个all-gather，Sequence并行相比没有引入更多的通信代价。一个使用reduce-scatter和all-gather实现all-reduce的Python代码示例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import torch
import torch.distributed as dist

# 初始化进程组
dist.init_process_group(backend='gloo')

# 获取进程组中的进程数和当前进程的排名
world_size = dist.get_world_size()
rank = dist.get_rank()

# 定义输入和输出张量
x = torch.tensor([1, 2, 3, 4])
result = torch.zeros_like(x)

# 使用 reduce_scatter 将每个进程的输入张量的部分和归约到每个进程的输出张量
dist.reduce_scatter(input_list=[x], output=result)

# 使用 all_gather 将每个进程的输出张量收集到所有进程中
output_list = [torch.zeros_like(result) for _ in range(world_size)]
dist.all_gather(output_list, result)

# 在每个进程上打印结果
print(f"Process {rank}: {output_list}")

# 清理资源
dist.destroy_process_group()

通过使用sequence parallel和tensor parallel以后，ActivationMemoryPerLayer相比公式(2)的值再次减少，相比公式(1)相当于对所有的ActivationMemory进行Tensor并行, 即 \(\frac{ActivationMemoryPerLayer}{t}\)：

\[\begin{gather} \begin{aligned} ActivationMemoryPerLayer &= sbh \left( \frac{10}{t} + \frac{24}{t} + 5 \frac{as}{ht} \right) \\ &= \frac{sbh}{t} \left( 34 + 5 \frac{as}{h} \right) \\ \end{aligned} \end{gather}\]

2.3 Pipeline Parallel

加上Pipeline Parallel后，对具有 \(L\) 层的layer的transformer来说，Pipeline Parallel并行度为 \(p\), 对应会分为 \(\frac{L}{p}\) 组(即stage个数)。以PipeDream中的1F1B调度为例，要完成初始化的话，第1个stage必须处理完 \(p\) 个micro-batch，让其他stage至少有1个micro-batch在处理，也就是要缓存 \(p\) 个micro-batch的activation。由于每个stage都有 \(\frac{L}{p}\) 个Layer，一共需要 \(p \times \frac{L}{p} = L\) 个layer的activation信息，对应总的计算如下：

\[\begin{gather} TotalActivationMemory = \frac{sbhL}{t} \left( 34 + 5 \frac{as}{h} \right) \\ \end{gather}\]

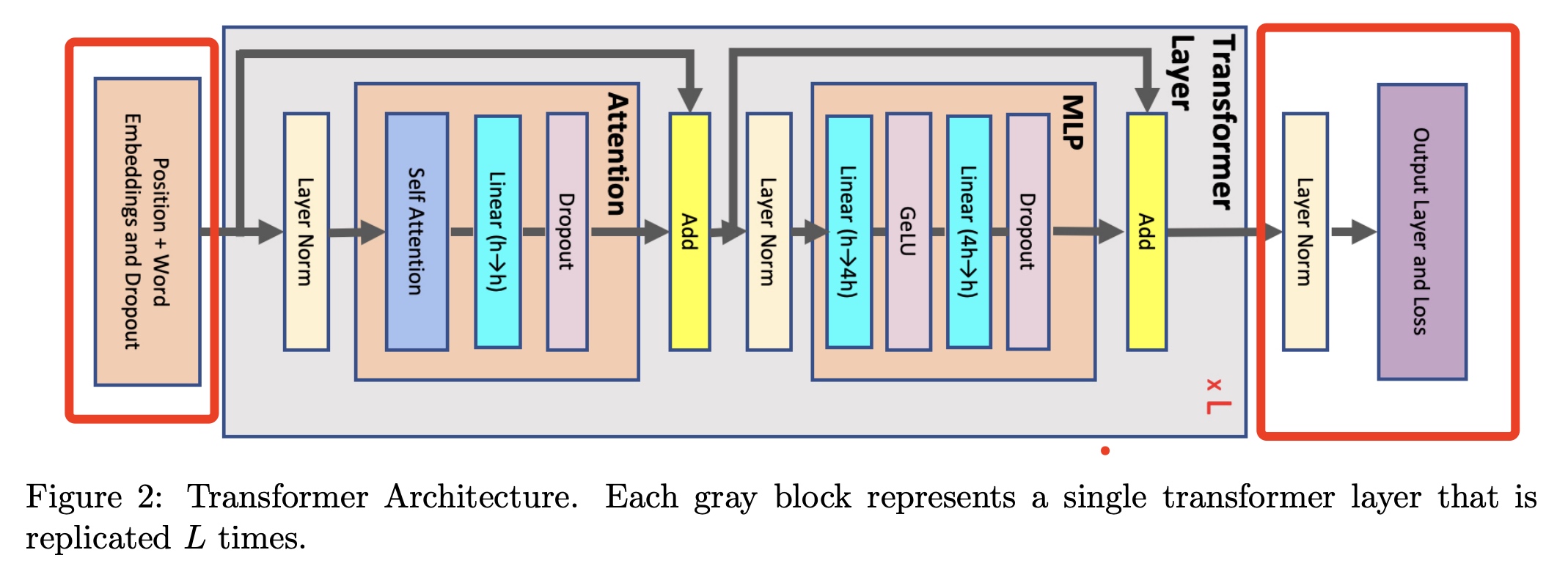
当然这里的公式(5)的ActivationMemory的计算没有加上EmbeddingLayer、最后的LayerNorm和输出的OutputLayer。加上这三部分的结果会略大于公式(5), 但以22B参数模型来说只增加0.01%的大小，这部分可忽略，证明请参考原论文。未计算部分如下图红色部分：

3. 可选Activation重计算介绍(Selective Activation Recomputation)

在后向过程中通过重计算方式重新计算前向结果来节省显存大小，这种方式文中称为full activation recomputation，以transformer为例会增加30%~40%的计算量。Selective的方式主要思路是选择 FLOPs 计算量小，且activation占用大的算子进行重计算，这里的 FLOPs 的衡量标准是GEMM的计算量大小。以公式(5)为例，针对大模型来说 \(5as/h \gt 34\), 如果重计算这部分layer的话可以减少快一半的activation大小。对于GPT-3来说，这种方式可以减少70%的activation显存大小，同时只增加了2.7%的 \(FLOPs\) 计算量。采用Selective Activation Recomputation后，公式(5)的结果可以减少为：

\[\begin{gather*} Total\ required\ memory = 34 \frac{sbhL}{t} \\ \end{gather*}\]

以下是不同方法组合下Activation Memory占用情况：

4. 参考