Rotary Position Embeddings论文阅读
1. 论文
1.1 Transformer中的position embedding
- Transformer中模型不涉及RNN的循环和CNN的卷积,为了学习到sequence中的前后顺序关系,增加了
position embedding, embedding的方法采用了sinine和cosine来进行。

- 示例如下, 对
I am a robot进行编码:
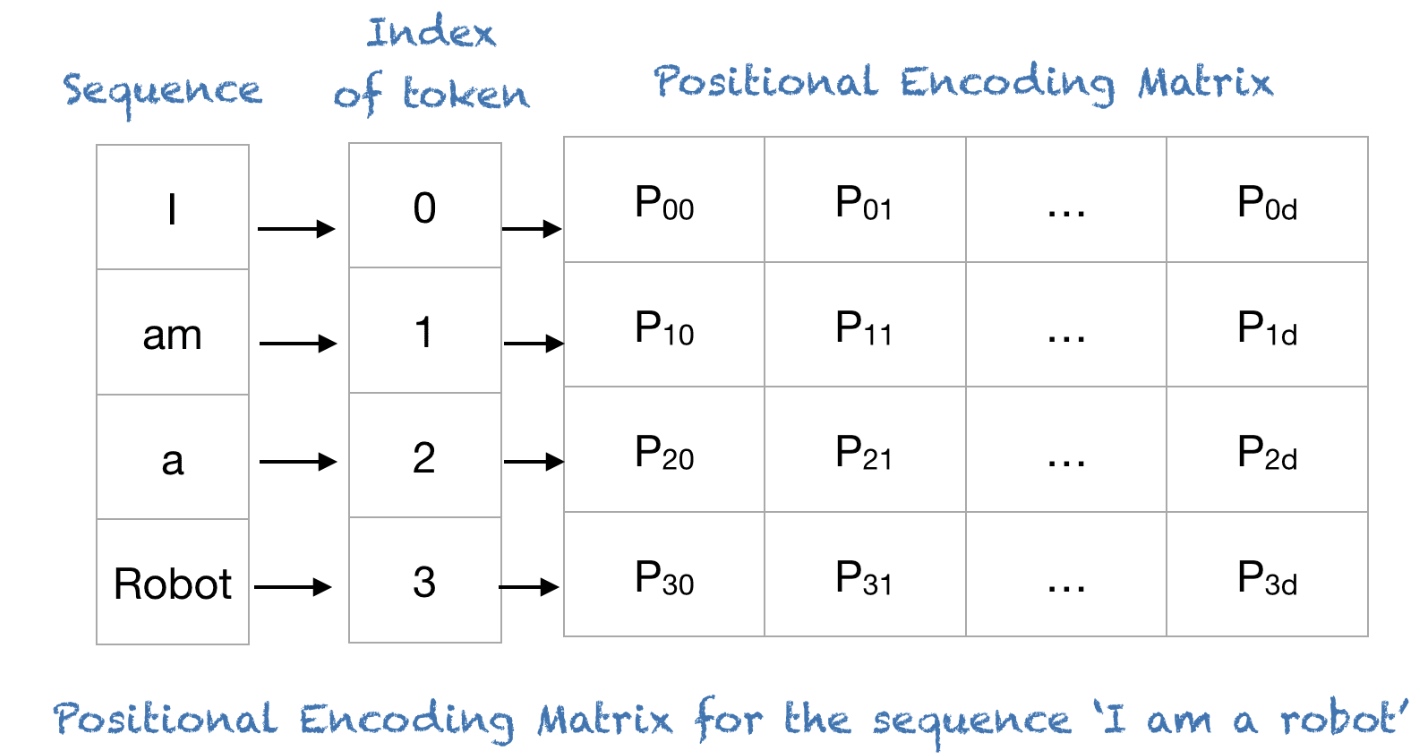
- 编码过程中d_model=4, 论文中的10000对应改为100,结果如下:

1.2 RoPE: Rotary Position Embeddings
1.2.1 绝对位置编码
- 在原始Transformer中采用的position
embedding是通过sine和cosine中计算出来的,加到对应的Q/K/V向量中,在文中称这种情况是绝对位置编码(
Absolute position embedding), 如下:
1.2.2 相对位置编码
对于相对位置编码(Relative position embedding)来说,有以下几种方式:
给Q/K/V向量加上可训练学习的相对位置编码向量,p_r是可通过训练学习的
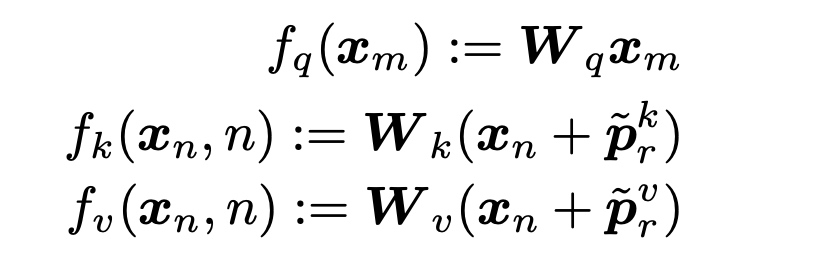
对QK的计算进行decompose分解,核心是通过p_(m-n)的相对编码替换绝对位置编码p_m
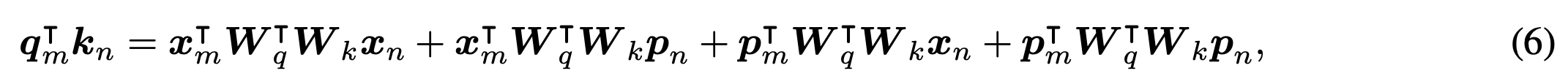
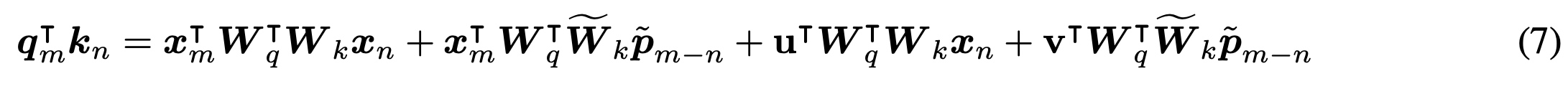
在2的基础上,使用不同的映射矩阵U来替换W

还是使用共同的W映射矩阵,唯一区别在于用
p_(m-n)相对距离替换p_m和p_n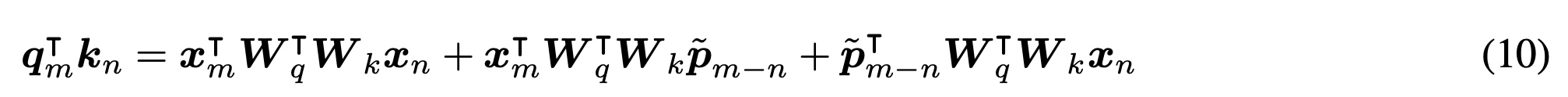
1.2.3 Rotary Position Embeddings
- q对应位置是m,k对应位置是n,RoPE编码要解决的问题中计算QK内积只依赖相对位置
m-n。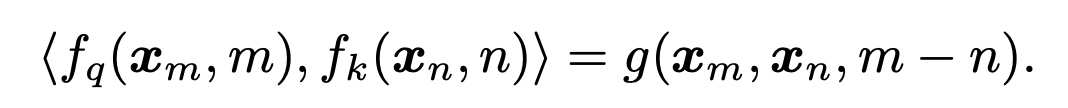
- 先考虑二维情况下的推导
- 使用复数的表示,Re表示计算结果中的复数部分
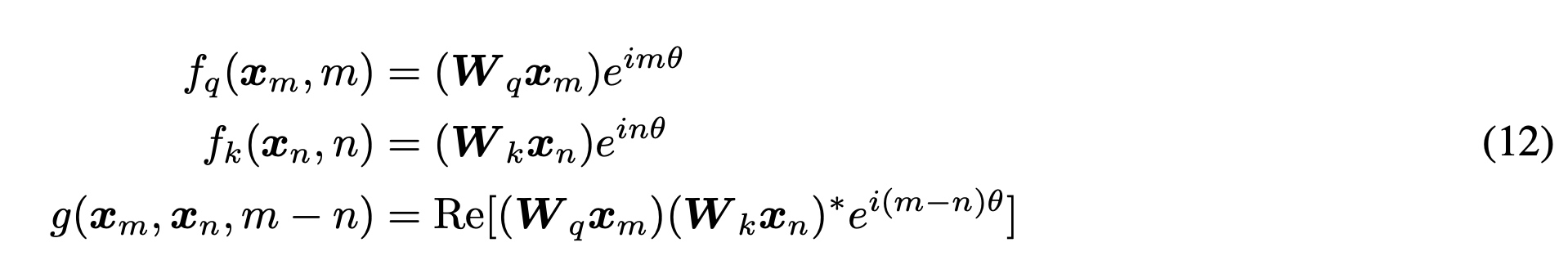
- 对应f(x_m,
m)写成如下,相对位置编码通过位置m和角度θ的旋转矩阵的乘积来表示。
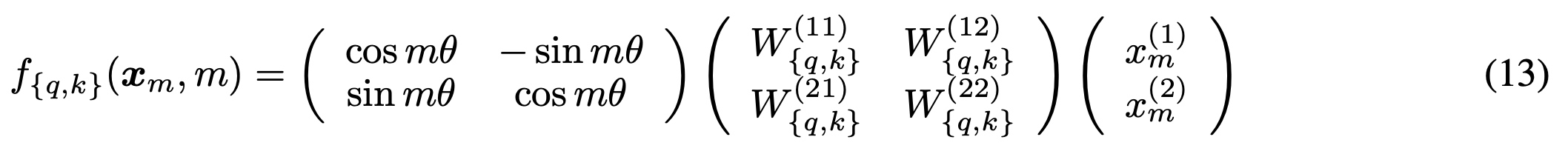
- 使用复数的表示,Re表示计算结果中的复数部分
- 更通用的形式
- 从二维扩到N维,对应的QK计算中相对位置只依赖R的矩阵
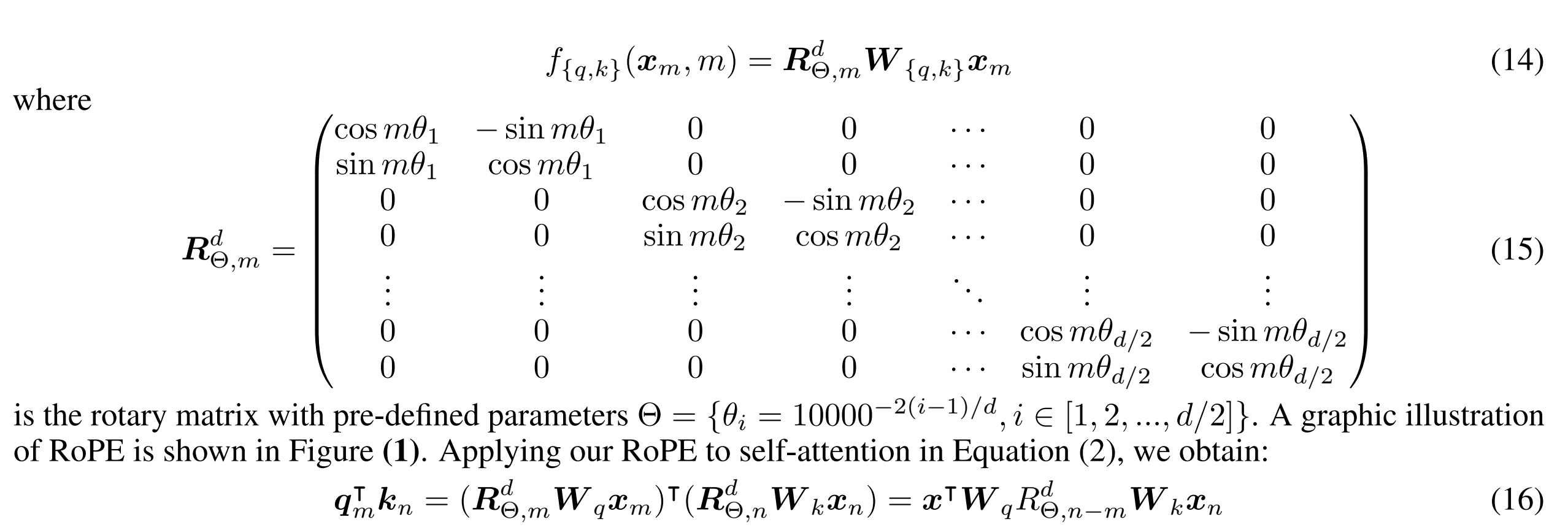
- 计算图更形象的展示如下
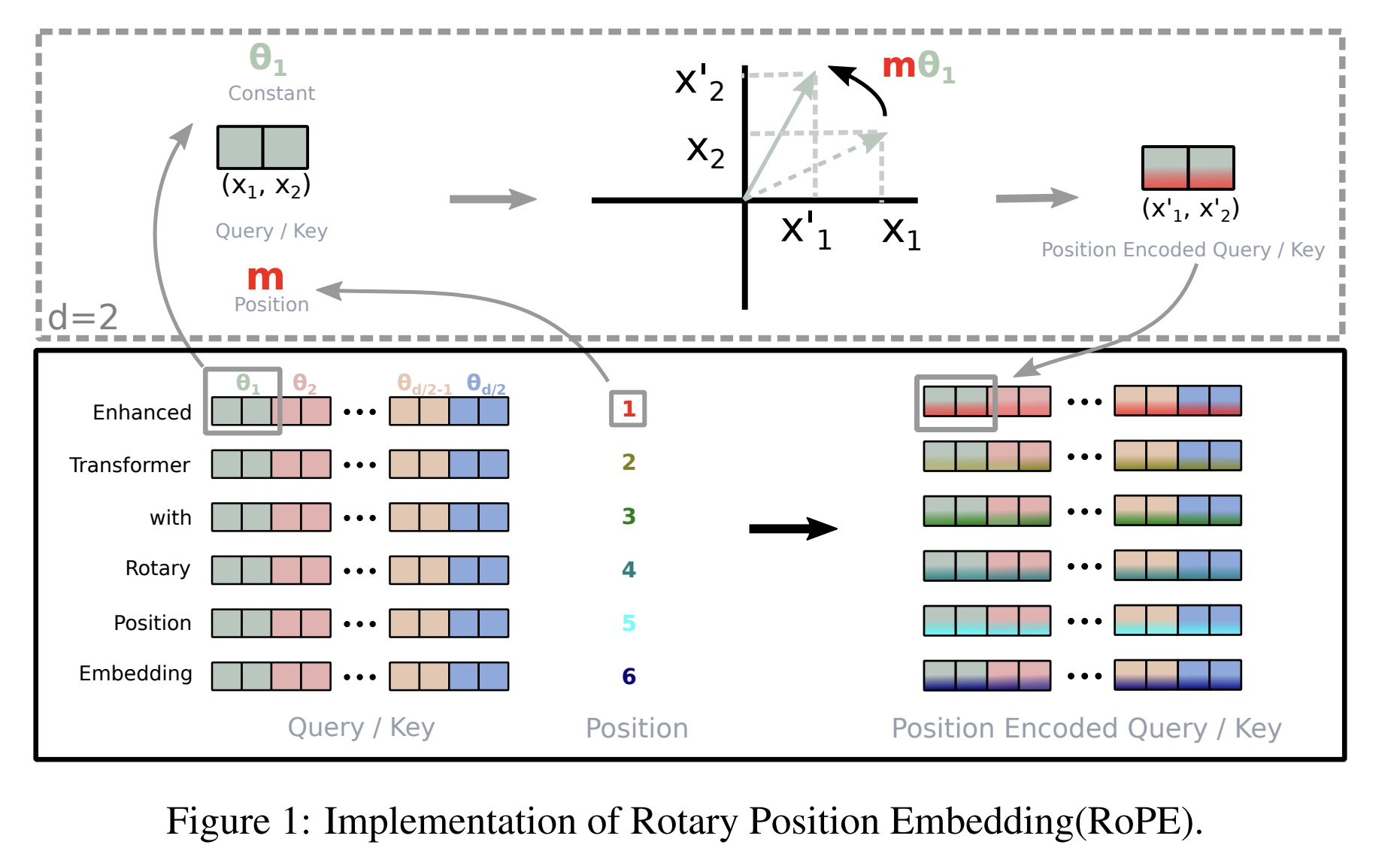
- 从二维扩到N维,对应的QK计算中相对位置只依赖R的矩阵
- PoRE的特性
- 距离衰减,QK的内积结果会随着相对距离增加而减少
- 支持线性Attention
- github实现示例
1 | sinusoidal_pos.shape = [1, seq_len, hidden_size] # Sinusoidal position embeddings |