RMSNorm论文阅读
1. 论文
1.1 RMSNorm介绍
RMSNorm论文中对LayerNorm的公式做了改造。在原有LayerNorm中借助了每个layer统计的mean和variance对参数进行了调整,但RMSNorm认为re-centering invariance property是不必要的,只用保留re-scaling invariance property。
LayerNorm的计算如下: 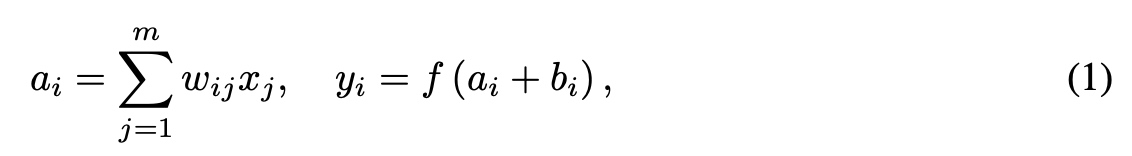
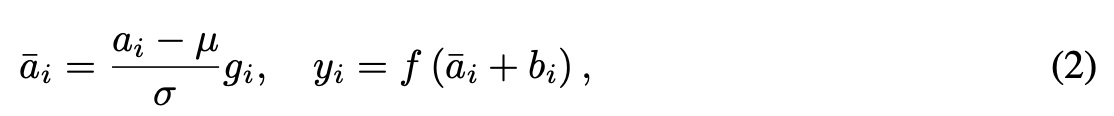
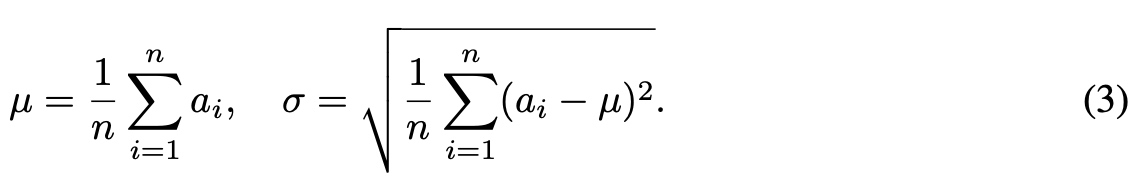
改造后的RMSNorm如下: 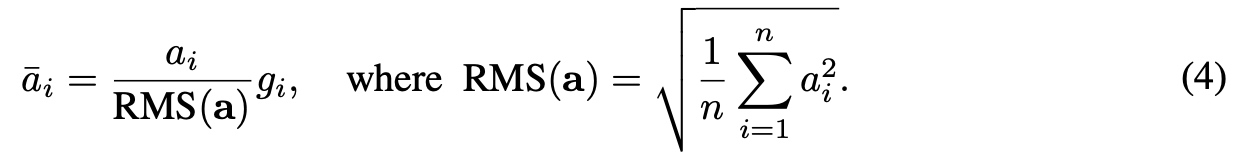 RMS中去除了
RMS中去除了mean的统计值的使用,只使用root mean square(RMS)进行归一化。
1.2 pRMSNorm介绍
RMS具有线性特征,所以提出可以用部分数据的RMSNorm来代替全部的计算,pRMSNorm表示使用前p%的数据计算RMS值。k=n*p表示用于RMS计算的元素个数。实测中,使用6.25%的数据量可以收敛

2. 其他Norm介绍
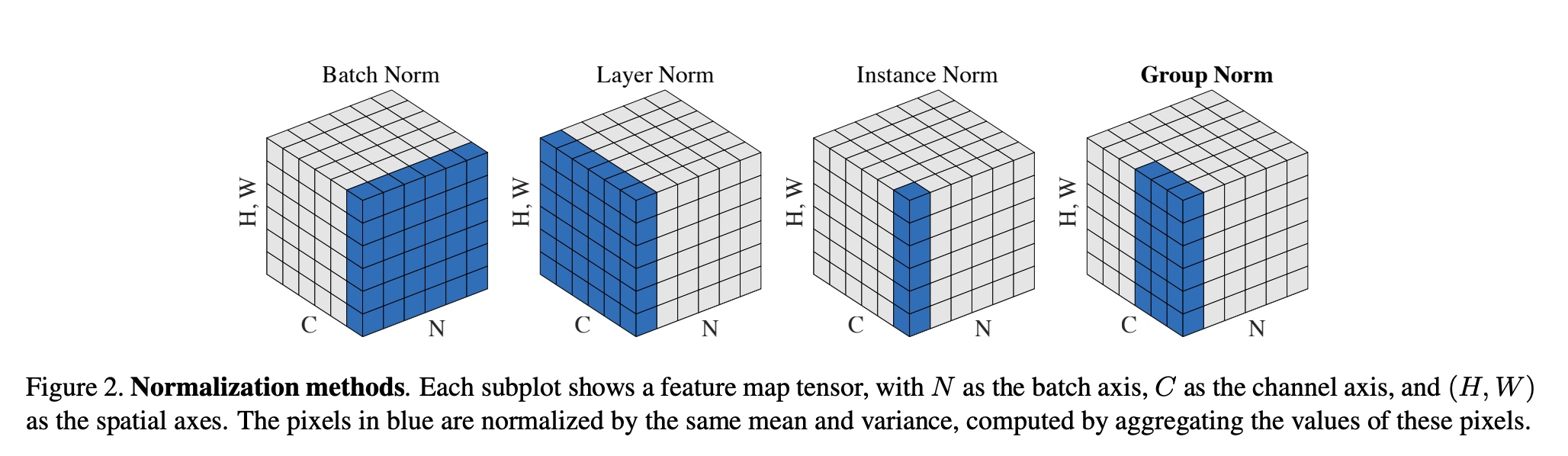
2.1 种类介绍
- BatchNorm:batch方向做归一化,算NHW的均值,对小batchsize效果不好;BN主要缺点是对batchsize的大小比较敏感,由于每次计算均值和方差是在一个batch上,所以如果batchsize太小,则计算的均值、方差不足以代表整个数据分布
- LayerNorm:channel方向做归一化,算CHW的均值,主要对RNN作用明显;
- InstanceNorm:一个channel内做归一化,算H*W的均值,用在风格化迁移;因为在图像风格化中,生成结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,因而对HW做归一化。可以加速模型收敛,并且保持每个图像实例之间的独立。
- GroupNorm:将channel方向分group,然后每个group内做归一化,算(C//G)HW的均值;这样与batchsize无关,不受其约束。
- SwitchableNorm是将BN、LN、IN结合,赋予权重,让网络自己去学习归一化层应该使用什么方法。
2.2 BatchNorm与LayerNorm的异同
- 对于二维矩阵来说,行为batch-size,列为样本特征。那么BatchNorm就是竖着归一化,LayerNorm就是横着归一化。
- 对于三维矩阵来说,BatchNorm是对除了channel维的所有参数做归一化,LayerNorm是对除了batch维的所有参数做归一化
- 如果你的特征依赖于不同样本间的统计参数,那BatchNorm更有效。因为它抹杀了不同特征之间的大小关系,但是保留了不同样本间的大小关系。(CV领域)
- NLP领域,LN就更加合适。因为它抹杀了不同样本间的大小关系,但是保留了一个样本内不同特征之间的大小关系。对于NLP或者序列任务来说,一条样本的不同特征,其实就是时序上字符取值的变化,样本内的特征关系是非常紧密的。