谱聚类算法介绍(Spectral Clustering)

发表于 2018-05-18 分类于机器学习本文字数： 4.3k 阅读时长 ≈ 16 分钟

这里先提前说下谱聚类的基本特征，然后后面按照论文的顺序做了讲解。 * 谱聚类算法与kmeans的区别，是把聚类的过程看成了一个图切割的过程，每一条样本都看成是N维空间内的一个节点，然后我们希望切割出来的子图，在子图内部点与点之前的距离(也就是相似度)会比较高，子图与子图之间的距离尽可能的小。 * 在谱聚类的过程中会把原始数据会做变换，从高维空间映射到低维空间，这样更容易进行聚类，可以看成向量化的过程。 * 矩阵的谱(spectrum)在数学中的定义表示是矩阵一系列的特征值。

图相关的基本概念

相似图(Similarity Graph)

推导符号说明

有一组数据节点 $x\_1, x\_2, ..., x\_n$，任意两个节点(例如 $x\_i, x\_j$ )之间的相似度(也就是距离)用 $S\_{ij}$ 来表示。
无向图的表示为 $G=(V, E)$，其中 $V={v\_1, v\_2, ..., v\_n}$ 中每一个 $v\_i$ 表示一个数据节点 $x\_i$, $E$ 表示节点与节点之间边的集合。
每条边都有一个权重值 $w\_{ij}$ 表示节点 $v\_i$ 与 $v\_j$ 之间的相似度，如果 $w\_{ij}$ 等于0表示两个节点是没有边进行连接的。
定义邻接矩阵（adjacency matrix）$W=(w\_{ij})\_{i,j=1,...n}$ 表示所有节点之间的距离，权重都是非负的(即 $w\_{ij} \ge 0$ ), 无向图中 $w\_{ij} = w\_{ji}$ 。
一个节点 $v\_i \in V$ 的度(degree) $d\_i$ 定义为$d\_i=\sum\limits\_{j=1}^{n}w\_{ij}$
定义度矩阵(degree matrix) $D$ 是由于 $d\_1, ..., d\_n$ 组成的对角矩阵；
定义指示矩阵(indicator matrix) $\mathbb{1}\_A = (f\_1,...,f\_n)' \in \mathbb{R}^n$ ，当节点 $v\_i \in A$ 时 $f\_i=1$, 否则 $f\_i=0$ ；
另外为了后面推导方便，再多定义一种简要写法: 用 $i \in A$ 代替写法 $ i | v_i A $，例如写一个求和公式的会用到: $\sum\_{i \in A}w\_{ij}$
$V$ 的两个子集($A, B \subset V$)之间的关系用 $W(A, B) := \sum\limits\_{i \in A, j \in B}w\_{ij}$，即A, B中任意两个节点的距离(相似度)之和。
衡量一个子集$A \subset V$ 的大小的方法有两种: 一种是用A中节点的个数($\|A\|$)表示，一种是用A中所有节点的度(degree)之和($vol(A) := \sum\limits\_{i \in A}d\_i$)表示
称一个子集 $A \subset V$ 是连通(connected)的意思表示A中任意两个节点都有边进行连接，以及这条连通边上的所有点也都在A这个子集中；称一个子集 $A \subset V$ 是连通分支(connected component)的意思是A是连通的，且$ A 与 A$ 之间没有边进行连接。(这里$\overline A$表示$\lbrace i| v\_i \in V, v\_i \notin A \rbrace$)

构建相似图的三种方法

$\varepsilon$距离相似图: 设置一个大小为$\varepsilon$的距离，然后分别计算两两节点之间的距离(相似度)，如果两两节点之间的距离小于$\varepsilon$，那么我们就把这两个节点连接在一起，因为节点之间距离是相互的，这个构建图是无向图。
k近邻相似图: 遍历每个节点，计算与当前节点相邻的距离最近的k个节点，然后把这k个节点和当前节点进行连接。这样的连接通常是有向图，因为A的k近邻节点包含B，但是B的k近邻节点不一定包含A。把有向图转成无向图有两种方法：（1）只要A的k近邻包含B或者B的k近邻包含A，就认为A和B是连通的（2）只有A的k近邻包含B且B的k近邻包含A，才认为A和B是连通的
全连接图: 连接所有节点, $X\_i$与$X\_j$节点之间的距离用$S\_{ij}$来表示，距离需要能够表示节点本身的距离范围，所以这里采用了高斯相似函数$ S(X_i, X_j) = exp(−||X_i - X_j||^2 / (2^2)) $

拉普拉斯图(Graph Laplacians)及其特性说明

谱聚类主要是基于拉普拉斯矩阵来做的，算法过程中会用到特征值的概念，特征值通常从小到大来进行排列，下面遇到的『前k个特征向量』通常是指前k小个特征值对应的特征向量。

非标准化的拉普拉斯矩阵

非标准化的拉普拉斯矩阵通常被定义为: \[L = D - W (D为度矩阵，W为相似矩阵)\]

示例如图所示(图片出处):

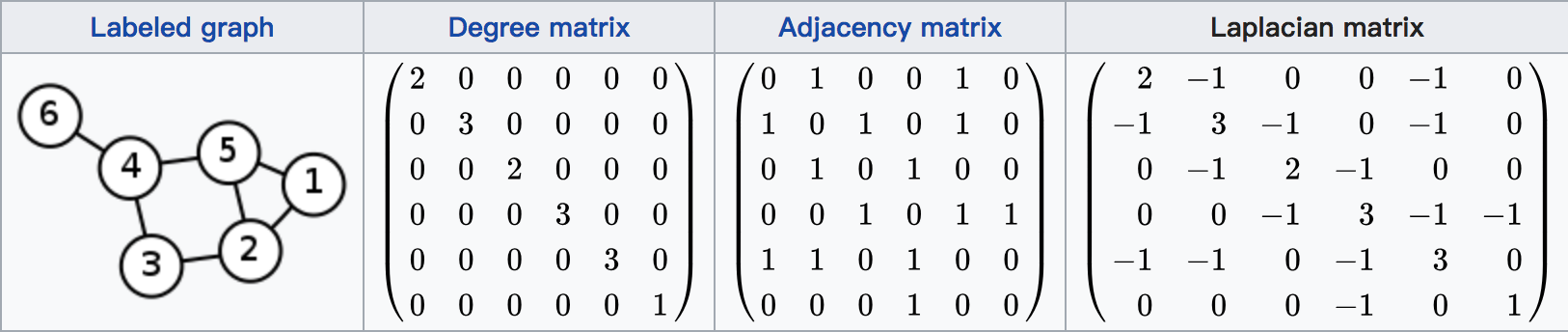
主张1 关于拉普拉斯矩阵L满足的性质

对于每一个向量$f \in \mathbb{R}^n$, 有下列等式成立:

\[ \begin{gather*} f'Lf = \frac{1}{2} \sum\limits\_{i,j=1}^n w\_{ij}(f\_i - f\_j)^2 \\ \end{gather*} \]

证明过程:

\[ \begin{gather*} f'Lf = f'Df - f'Wf = \sum\limits\_{i=1}^n d\_{i}f\_{i}^2 - \sum\limits\_{i,j=1}^n f\_{i}f\_{j}w\_{ij} \\ = \frac{1}{2} \left ( \sum\limits\_{i=1}^n d\_{i} f\_{i}^2 - 2 \sum\limits\_{i,j=1}^n f\_{i} f\_{j} w\_{ij} + \sum\limits\_{j=1}^n d\_{j} f\_{j}^2 \right ) \\ = \frac{1}{2} \left ( \sum\limits\_{i,j=1}^n w\_{ij} (f\_i - f\_j)^2 \right ) \\ \end{gather*} \]

L矩阵是对称的, 且是半正定的

证明过程: 因为矩阵W和D都是对称的，所以求得的L也是对称的。因为对于所有的$ f ^n，存在f'Lf $，所以L是半正定的,证毕。
L矩阵最小的特征值是0，0对应的特征向量是$ $常数向量(constant vector)，即向量中所有的值都是常数，且为1

证明过程: 等式$ f'Lf = 0 $ 成立，这里f为$ $常数向量,证毕。
L有n个非负数的实数特征值，$ 0 = _1 _2 ... _n $

主张2 关于拉普拉斯矩阵L中连通分支的个数与矩阵的谱

定义G为一个无向图，无向图中所有权重都是非负的。如果无向图的拉普拉斯矩阵L的0特征值出现的次数(multiplicity)为k，那么图中连通分支($ A_1, A_2, ..., A_n $)的个数也为k。这些特征值0对应的特征指示向量为$ _{A_1},...,_{A_n} $

证明过程: 我们先假设$ k=1 $ 的情况，当 $ k=1 $ 时图是连通的(注意这里不是连通分支，连通和连通分支是不同概念)，f是特征值为0对应的特征矩阵。于是我们有

\[ \begin{gather*} 0 = f'Lf = \sum\limits\_{i,j=1}^{n} w\_{ij}(f\_i - f\_j)^2 \\ \end{gather*} \]

这里因为 $ w_{ij} $ 是非负的，如果这里 $ w_{ij} $ 的话，要想上面等式成立的话要有$ f_i = f_j $，所以这里f需要是一个常数向量才能实现。又因为连通矩阵中任意两两节点都有连接，所以需要等式成立的话，f必须是一个$ $常数向量，f也是L矩阵的指示向量。
现在开始考虑 $ k > 1 $的情况，这时我们手动把原始所有节点根据它们所属的连通分支进行重新排序以后，邻接矩阵$ W $可以得到一个对角块矩阵的形式，同样拉普拉斯矩阵$ L $也是一个对角块矩阵的形式，如下图所示:

\[ \left ( \begin{array}{rrrr} & L\_1 & & & \\\\ & & L\_2 & & \\\\ & & & \cdot\cdot\cdot & \\\\ & & & & L\_k \\\\ \end{array} \right ) \]

每一个$ L_i $都是一个连通分支(满足子集合内部两两节点有连线，且连通分支与连通分支之间没有连线)。

__L矩阵的谱(特征值)是各个子集$ L_i $的谱组成的__，证明过程如下: 根据特征向量的性质，具有特征值为$ $的块矩阵A满足下列等式:

\[ det \left ( \begin{array}{rr} & B-\lambda I & C \\\\ & 0 & D-\lambda I \\\\ \end{array} \right ) \]

根据行列式的性质可以得到:

\[ det \left ( \begin{array}{rr} & B-\lambda I & C \\\\ & 0 & D-\lambda I \\\\ \end{array} \right ) = det(B - \lambda I) det(D - \lambda I) = 0 \]

可以看出B与D的特征值也都是A的特征值，证毕。

最后从上述也可以看出，特征值0的个数就等于连通分支子图的个数，特征向量f就是连通分支子图的指示向量。

标准化(normalized)的拉普拉斯矩阵

标准化的拉普拉斯矩阵通常被定义为:

\[ \begin{gather*} L\_{sym} := D^{-\frac{1}{2}} L D^{\frac{1}{2}} = I - D^{\frac{1}{2}} W D^{-\frac{1}{2}} \\ L\_{rw} := D^{-1} L = I - D^{-1} W \\ \end{gather*} \]

这里D为度矩阵，W为相似矩阵, $L_{sym} $处理完是对称矩阵，$L_{rw} $跟随机游走的方法很相似。下面列出一些标准化拉普拉斯矩阵的性质。

主张3 $L\_{sym} 与 L\_{rw}矩阵的性质$

对于每一个$ f ^n$，都有

\[ \begin{gather*} f'L\_{sym} f = \frac{1}{2} \sum\limits\_{i,j=1}^n w\_{ij} \left ( \frac{f\_i}{\sqrt{d\_i}} - \frac{f\_j}{\sqrt{d\_j}} \right )^2 \\ \end{gather*} \]

证明过程可参考 <主张1> 中证明，这里$ D D^{-}, d_i $

$ 和分别是 L_{rw} 的特征值和特征向量，当且仅当 L_{sym} 的特征向量也是 , 特征向量是 w = D^{} $
$ 和分别是 L_{rw} 的特征值和特征向量，当且仅当和满足泛化的特征问题 L = D $
$ L_{rw}的特征值为0时，特征向量是常数向量；L_{sym}的特征值为0时，特征向量是D^{} $
$ L_{rw} 和 L_{sym} 都是半正定的，具有非负实数特征值 0 = _{1} _{2} ... _{n} $

主张4 关于连通分支的个数以及$ L_{sym} $ 和 $ L_{rw} $ 的谱

G是一个无向图，$ L_{rw} $ 和 $ L_{sym} $ 值为0的特征值的个数等同于连通分支($ A_1, , A_k $)的个数。对于$ L_{rw} $ 0特征值对应的指示矩阵为$ _{A_i} $, 对于 $ L_{sym} $ 0特征值对应的指示矩阵为$ D^{} _{A_i} $

谱聚类算法描述

非标准化(unnormalized)的谱聚类

过程:
输入矩阵$ S R^{n n} $构建相似图, 创建W为邻接矩阵， D为度矩阵计算非标准化的拉普拉斯矩阵L, L=D-W 计算矩阵L的前k小的特征值对应的特征向量输出矩阵$ U R^{n k} $，输入的每个节点的表示就都转化成了k维向量，U矩阵中的每一行都表示一个节点把所有的节点通过k-means方法进行聚类产出$ A_1, A_2, …, A_n $结果

标准化(normalized)的谱聚类

算法1

过程:
输入矩阵$ S R^{n n} $构建相似图, 创建W为邻接矩阵， D为度矩阵计算非标准化的拉普拉斯矩阵L, L=D-W ** 计算$ L = D $的前k小的特征值对应的特征向量（实际上求的是$ L_{rw} $的特征向量）** 输出矩阵$ U R^{n k} $，输入的每个节点的表示就都转化成了k维向量，U矩阵中的每一行都表示一个节点把所有的节点通过k-means方法进行聚类产出$ A_1, A_2, …, A_n $结果

算法2

过程:
输入矩阵$ S R^{n n} $构建相似图, 创建W为邻接矩阵， D为度矩阵计算非标准化的拉普拉斯矩阵L, L=D-W ** 计算$ L = D $的前k小的特征值对应的特征向量（实际上求的是$ L_{rw} $的特征向量）** 输出矩阵$ U R^{n k} $，输入的每个节点的表示就都转化成了k维向量，U矩阵中的每一行都表示一个节点 ** 将U矩阵中每一行作归一化, 然后生成新的矩阵T ** 把所有的节点通过k-means方法进行聚类产出$ A_1, A_2, …, A_n $结果

示例说明

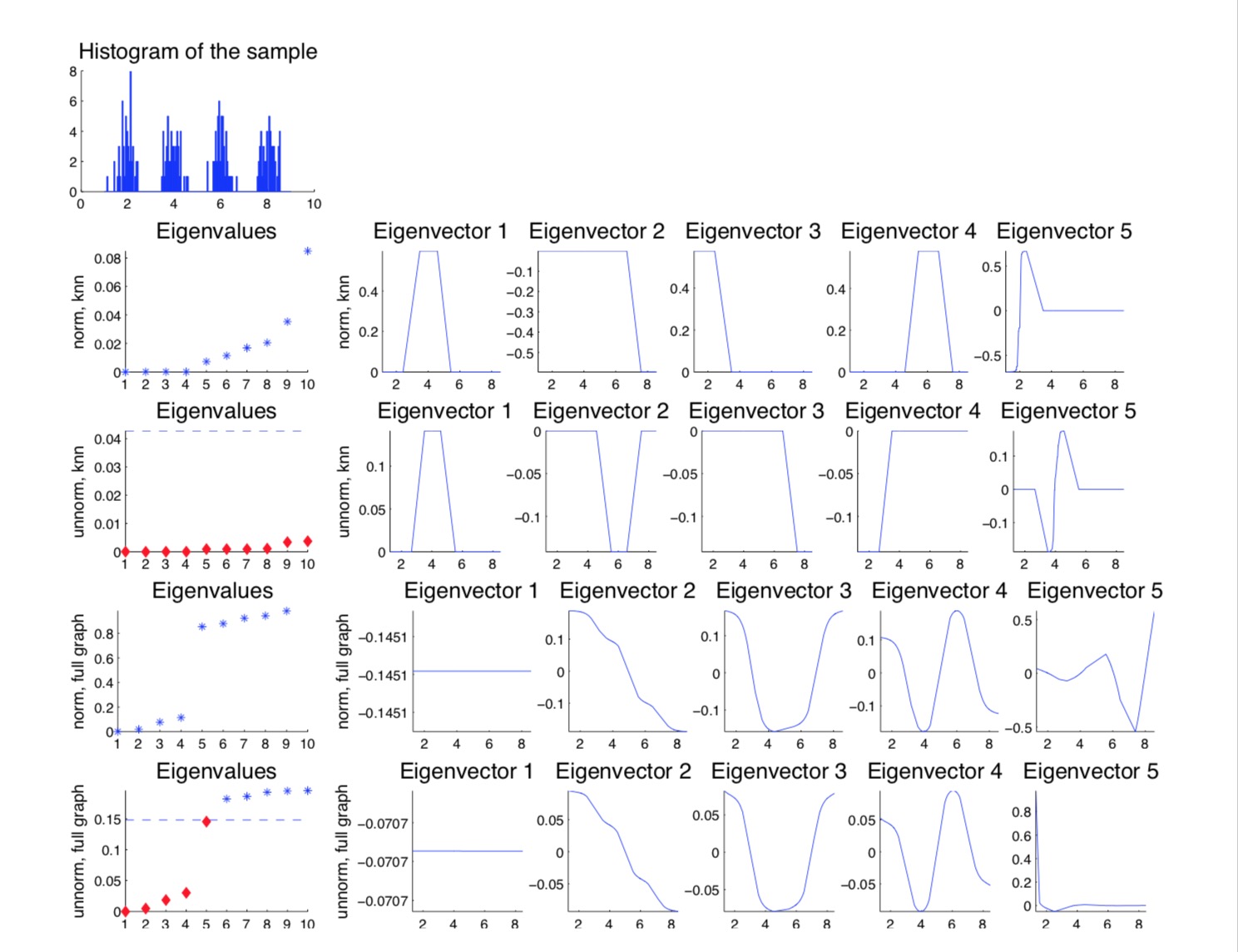
文中给了一个示例，通过4种混合高斯方法随机生成大约200个节点进行谱聚类。图第一行是这200个节点（$ x_i, y_i $）的条形分布，x,y轴分别表示节点的位置距离。接下来2,3行是k近邻相似图的标准和非标准化拉普拉斯矩阵的特征值和特征向量，4，5行是全连接相似图的标准和非标准拉普拉斯矩阵的特征值和特征向量。特征值的横坐标是特征值的索引，纵坐标是特征值的value；特征向量图的横坐标含义是$ x_i $，纵坐标是特征向量的实数值。第二行中有4个特征值为0，根据之前的推导可以知道该矩阵中存在4个连通分支，且每个特征值为0的特征向量都是这个矩阵的指示向量。从第三行中第二个特征向量从0的位置画一条横线，能把聚类的簇1，4和簇2，3区分出来，类似的，第三个特征向量的图中从0的位置画一条横线，可以把簇1，4和簇2，3区分开来。能区分以后就可以通过聚类的方式来进行类别的检测了。

图切分角度来谈谱聚类算法

谱聚类的初衷就是为了把图中的节点按照他们的相似度进行切分成不同的组，最终希望可以达到组内两两节点之间的连线权重越高越好，而组与组($ A_1,,A_k $)之间的连线权重越低越好。用形式化的表示即:

\[ \begin{gather*} min cut(A\_1, \dots, A\_k) := \frac{1}{2} \sum\limits\_{i=1}^k W(A\_i, \overline A\_i) \\ \end{gather*} \]

这里乘上$ $是因为无向图权重会被重复计算两次。按照这种最小化切割出来的图经常会碰到单个节点被切割出来的情况，为了解决这种情况，通过下列两种方式对上述公式进行了优化。

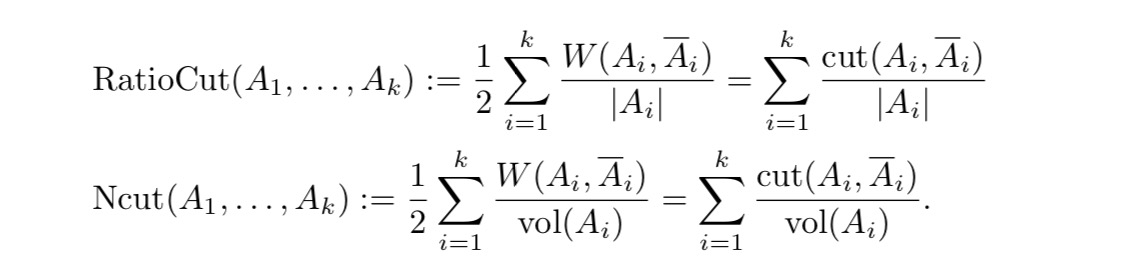
这里$ |A_i| $表示$ A_i $集合中节点的总个数，$ vol(A_i) $ 表示$ A_i $集合中所有边上权重加和。当$ A_i $中包含了所有节点的时候，上述两个等式才是最小的。

图切分只有两类(k=2)时RatioCut的情况

我们的目标是 > $ _{A V} RatioCut(A, A) $

定义向量$ f=(f_1,,f_n)' R^n $为下列等式: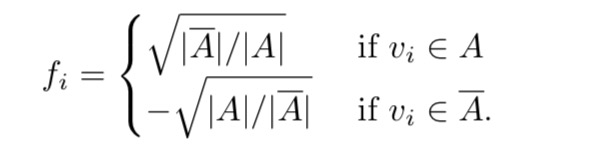

定义完f以后有下列几个等式成立: 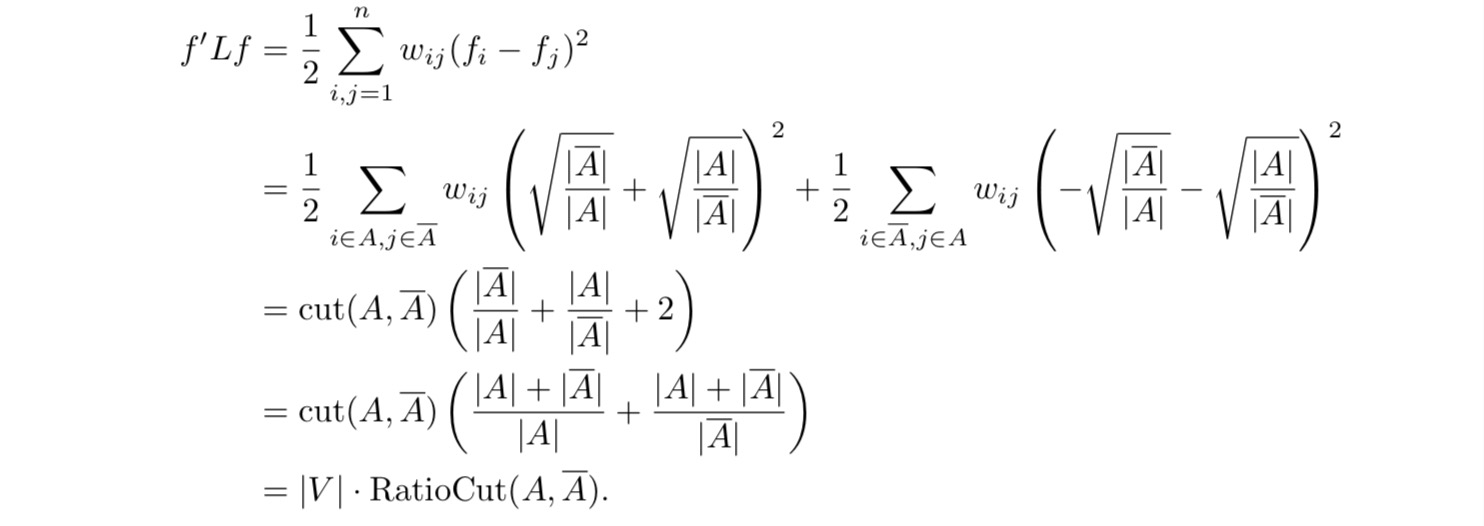可以看出把$ min RatioCut(A, A) $等价为优化 $ min f'Lf $

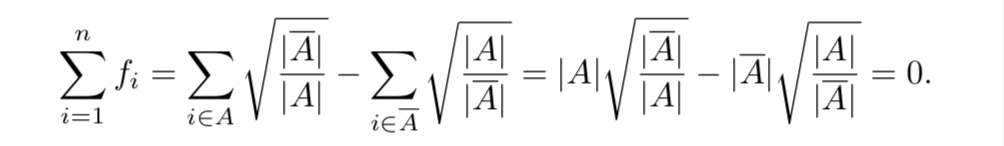可以看出f向量正交于$ $常数向量

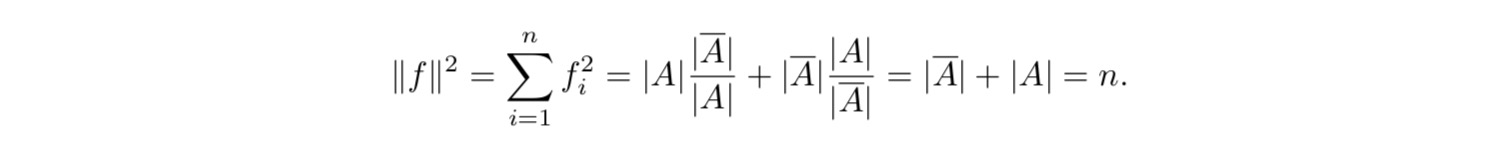可以看出$ ||f|| = $

汇总上面的出来的信息得到优化整体目标: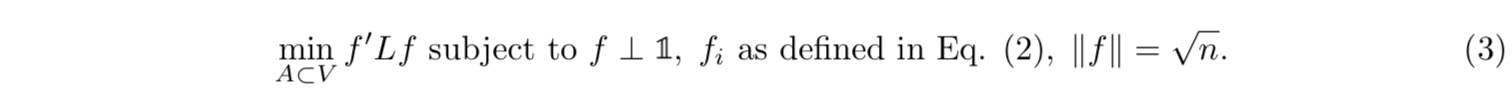

上面的优化目标只针对f属于两个值，我们可以把f的取值再次进行扩展，不限制f的取值即可以得到下面的优化目标:

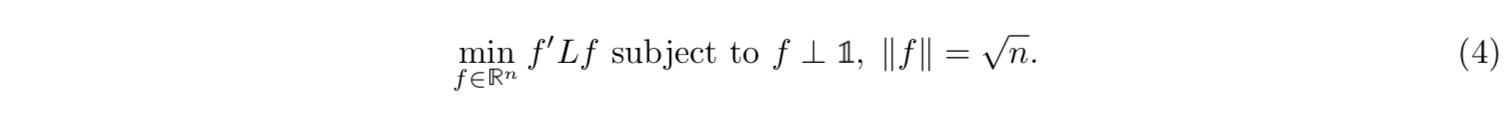
求解$ f'Lf $的特征向量非常困难, 通过[Rayleigh-Ritz 理论](https://en.wikipedia.org/wiki/Rayleigh%E2%80%93Ritz_method)求的近似解。Rayleigh-Ritz理论告诉我们如果求解$ Ax = x$困哪的话，可以通过$ R V^* A V $变换以后，求解$ Rv_i = _i v_i $，最终得到Ritz对 $ (_i, _i) = (_i, Vv_i)$。所以我们这里可以先求得L矩阵的前k小的非0的特征值对应的特征向量(即指示向量f)。对于二分类的话，通过指示向量我们可以用下面的规则来进行类别判断: 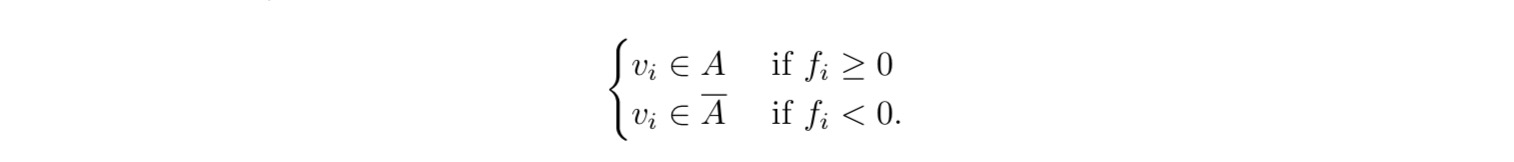对于多分类的话，指示向量可以通过属于多个范围来进行类别的划分: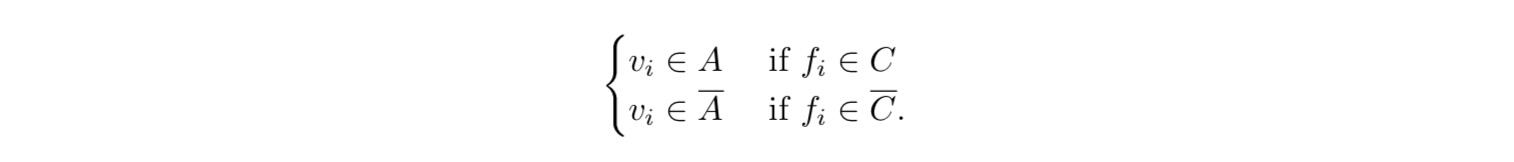

这里其实就是非规则化的谱聚类算法的初衷，因为规则化的谱聚类算法跟非规则化非常相似这里不在赘述，详情可以参见论文A Tutorial on Spectral Clustering。规则化两种算法的区别这里说下因为算法2没有归一化的话可能会因为权重太小造成最终的效果不准确，所以为了避免遇到权重过下的情况这里多做了一次归一化的操作，扰动理论可以参见这里。而算法1本身是采用的随机游走$L\_{rw}$的方式来进行的，其实在除以节点数的时候就已经算是做了归一化了，所以不用再额外来做。