LLM大模型训练加速利器FlashAttention详解
1. 背景介绍
因为Transformer的自注意力机制(self-attention)的计算的时间复杂度和空间复杂度都与序列长度有关,所以在处理长序列的时候会变的更慢,同时内存会增长更多。通常的优化是针对计算复杂度(通过\(FLOPs\) 数衡量), 优化会权衡模型质量和计算速度。
在FlashAttention中考虑到attention算法也是IO敏感的,通过对GPU显存访问的改进来对attention算法的实现进行优化。如下图,在GPU中片上存储SRAM访问速度最快,对应的HBM(high
bandwidth memory)访问速度较慢,为了加速要尽量减少HBM的访问次数。 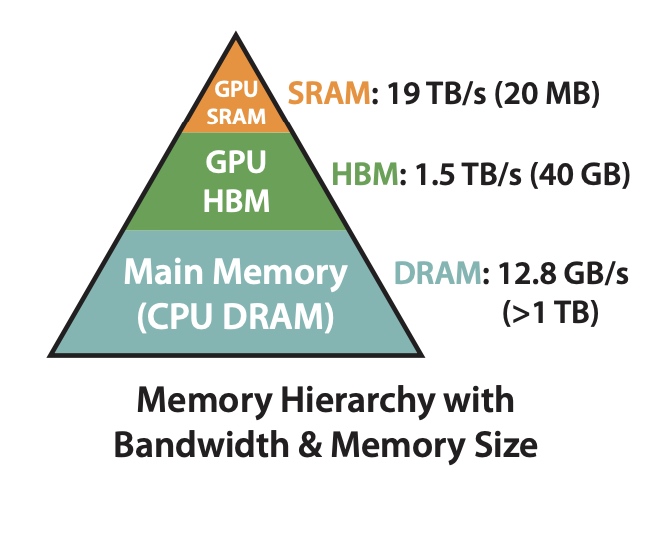
2. 详细解读
2.1 标准的attention算法实现
首先回顾下标准的attention算法实现,有 \(Q, K, V\) 三个矩阵,计算有以下三步,都是跟HBM交互:
\[ \begin{gather*} S = QK^T \\ P = softmax(S) \\ O = PV \end{gather*} \]

2.2 FlashAttention算法实现
FlashAttention算法实现的关键在于以下三点: 1. softmax的tiling展开,可以支持softmax的拆分并行计算,从而提升计算效率 2. 反向过程中的重计算,减少大量的显存占用,节省显存开销。 3. 通过CUDA编程实现fusion kernel
2.2.1 softmax展开(tiling)
- 基本softmax。在计算 \(x_i\) 的值的时候需要用到所有的 \(X=\{x_1, ..., x_N\}\) 值,计算公式如下:
\[ \begin{gather*} X = \left[ x_1, ..., x_N \right] \\ f(X) = \left[ e^{x_1}, ..., e^{x_N} \right] \\ l(X) = \sum f(X) \\ softmax(X) = \frac{f(X)}{l(X)} = softmax({x_1, ..., x_N}) = \left\{ \frac{e^{x_i}}{\sum^N_{j=1}e^{x_j}} \right\}^N_{i=1} \\ \end{gather*} \]
- 安全(safe) softmax。由于 \(e^{x_i}\) 很容易溢出, 比如FP16支持范围是
\(2^{-24} \sim 65504\) ,当 \(x_i \ge 11\) 的时候,\(e^{x_i}\)
会超过float16的有效位。为解决这个问题提出
safesoftmax, 对每个 \(x_i\) 都减去一个 \(m = max^N_{j=1}(x_j)\) , 使得 \(x_i - m \ll 0\), 这时幂操作符对负数输入的计算是准确且安全的。
\[ \begin{gather*} m(X) = max^N_{j=1}(x_j) softmax(X) = \frac{e^{x_i - m(X)}}{\sum_{j=1}^{N}e^{x_j - m(X)}} m(X) = max^N_{j=1}(x_j) \end{gather*} \]
- Safe softmax tiling。对于 \(X\) 分为两组情况进行说明,其中 \(X=\left[ X^{(1)}, X^{(2)}\right]\) 。
\[ \begin{gather*} m(X) = m(\left[ X^{(1)}, X^{(2)} \right]) = max(m(X^{(1)}), m(X^{(2)})) \\ f(X) = \left[ e^{m(X^{(1)}) - m(X)} f(X^{(1)}), e^{m(X^{(2)}) - m(X)} f(X^{(2)}) \right] \\ l(X) = l(\left[ X^{(1)}, X^{(2)} \right]) = e^{m(X^{(1)}) - m(X)}f(X^{(1)}) + e^{m(X^{(2)}) - m(X)} f(X^{(2)}) \\ softmax(X) = \frac{f(X)}{l(X)} \\ \end{gather*} \]
- safe softmax基本计算示例
\[ \begin{gather*} X = \left[ 1, 2, 3, 4 \right]\\ m(X) = 4\\ f(X) = \left[ e^{1-4}, e^{2-4}, e^{3-4}, e^{4-4} \right] \\ l(X) = \sum f(X) \\ softmax(X) = \frac{f(X)}{l(X)} \\ \end{gather*} \]
- safe softmax tiling计算示例(结果跟基本计算示例一致)
\[ \begin{gather*} X = \left[ 1, 2, 3, 4 \right] = \left[ X^{(1)}, X^{(2)} \right], m(X) = 4 \\ X^{(1)} = \left[ 1, 2 \right], m(X^{(1)}) = 2 \\ X^{(2)} = \left[ 3, 4 \right], m(X^{(2)}) = 4 \\ f(X^{(1)}) = \left[ e^{1-2}, e^{2-2} \right] \\ f(X^{(2)}) = \left[ e^{3-4}, e^{4-4} \right] \\ f(X) = \left[ e^{2-4}f(X^{(1)}), e^{4-4}f(X^{(2)}) \right] = \left[ e^{1-4}, e^{2-4}, e^{3-4}, e^{4-4} \right] \\ l(X) = \sum f(X) \\ softmax(X) = \frac{f(X)}{l(X)} \\ \end{gather*} \]
有了softmax tiling的基础以后,在执行的时候可以对 \(Q、K、V\) 三个矩阵进行分块操作并行计算了。
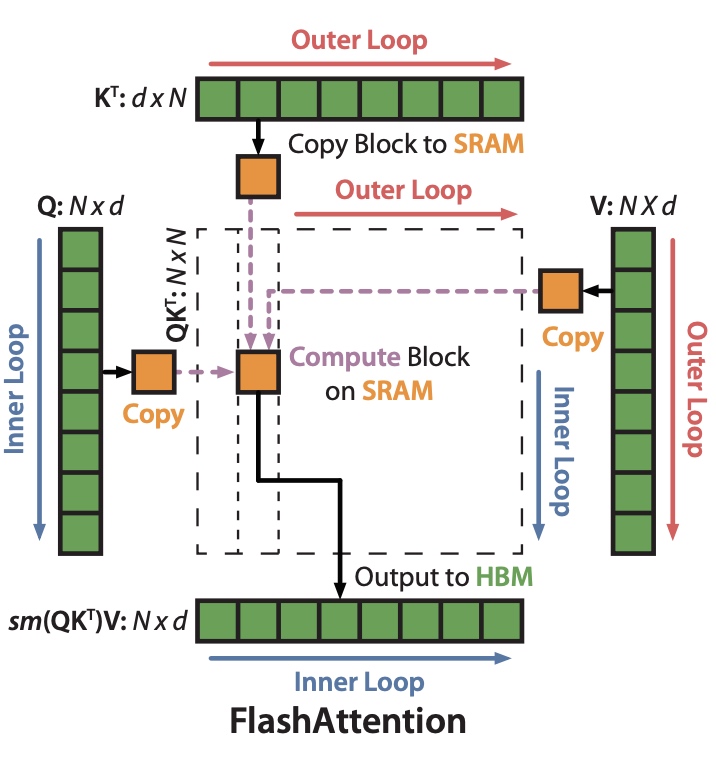
2.2.2 反向过程中的重计算
类似于gradient checkpoint方法,在前向的时候把输出结果 \(O = softmax(QK^T)V、l、m\)
存入HBM中, 在反向时候重新计算需要的数据。
2.2.3 最终完整的算法说明如下:

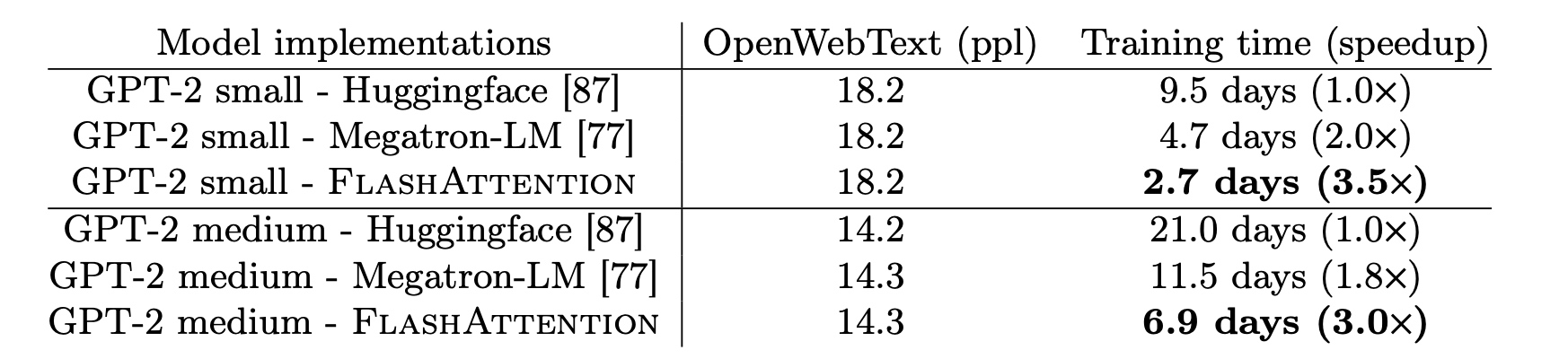
2.2.4 结果展示