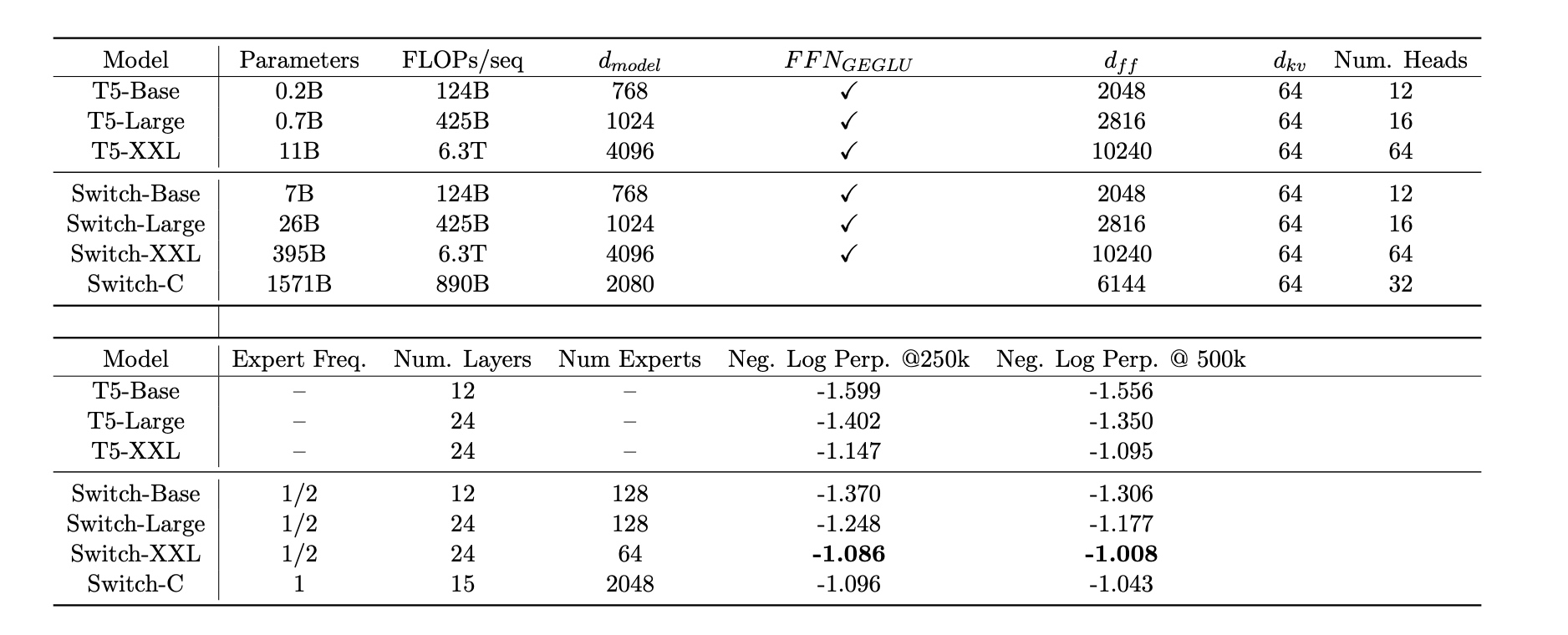
MOE论文详解(3)-Switch Transformers:Scaling to Trillion Parameter Models with Simple and Efficient Sparsity

发表于 分类于 本文字数： 3k 阅读时长 ≈ 11 分钟

Switch Transformers也是google在2022年发表的一篇论文, 该论文简化了MoE的路由算法, 减少了计算量和通信量; 第一次支持bfloat16精度进行训练. 基于T5-Base和T5-Large设计的模型在相同的算力下训练速度提升了7x倍; 同时发布了1.6万亿(1.6 trillion)参数的MoE模型，相比T5-XXL模型训练速度提长了4x倍.

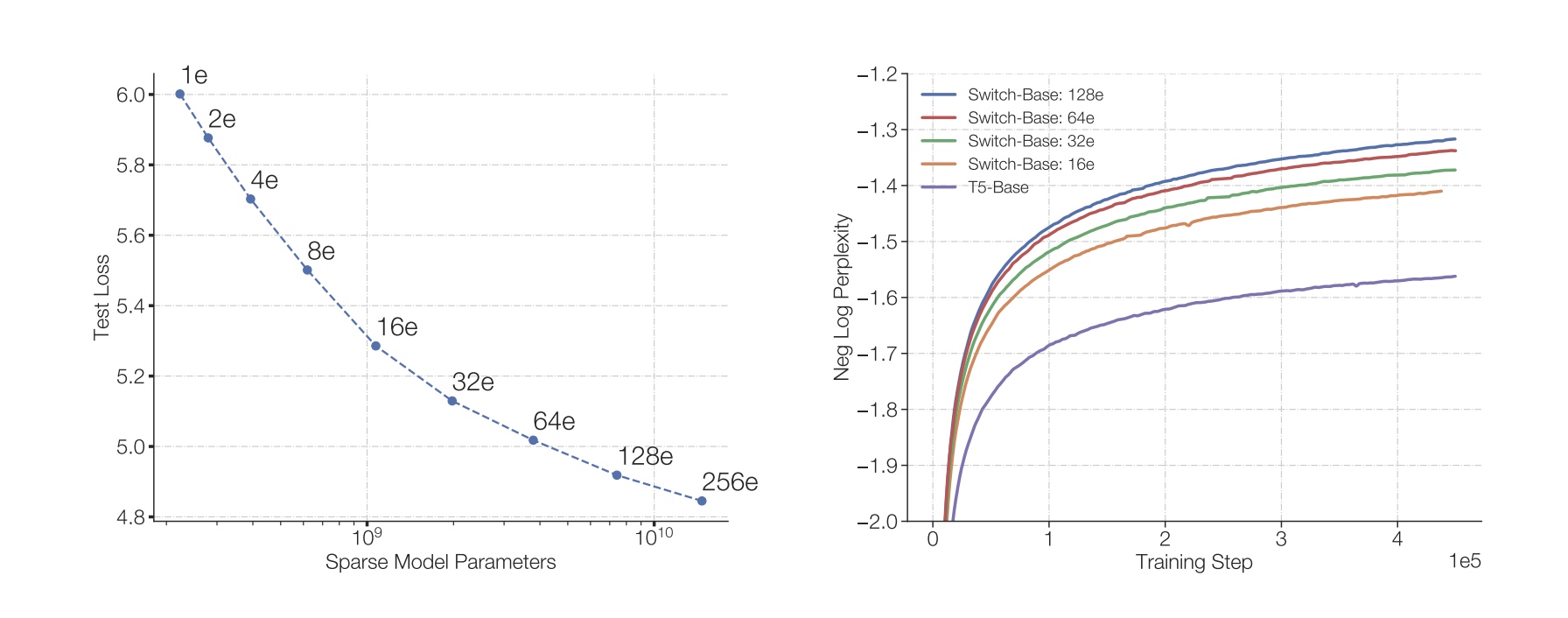
左边图中表示不同专家个数对应的参数量与loss这间的关系, 专家数越多对应的参数量越大, loss越低; 右边图中在相同训练step下比较不同模型的负对数困惑度（Negative Log Perplexity）

1. 模型介绍

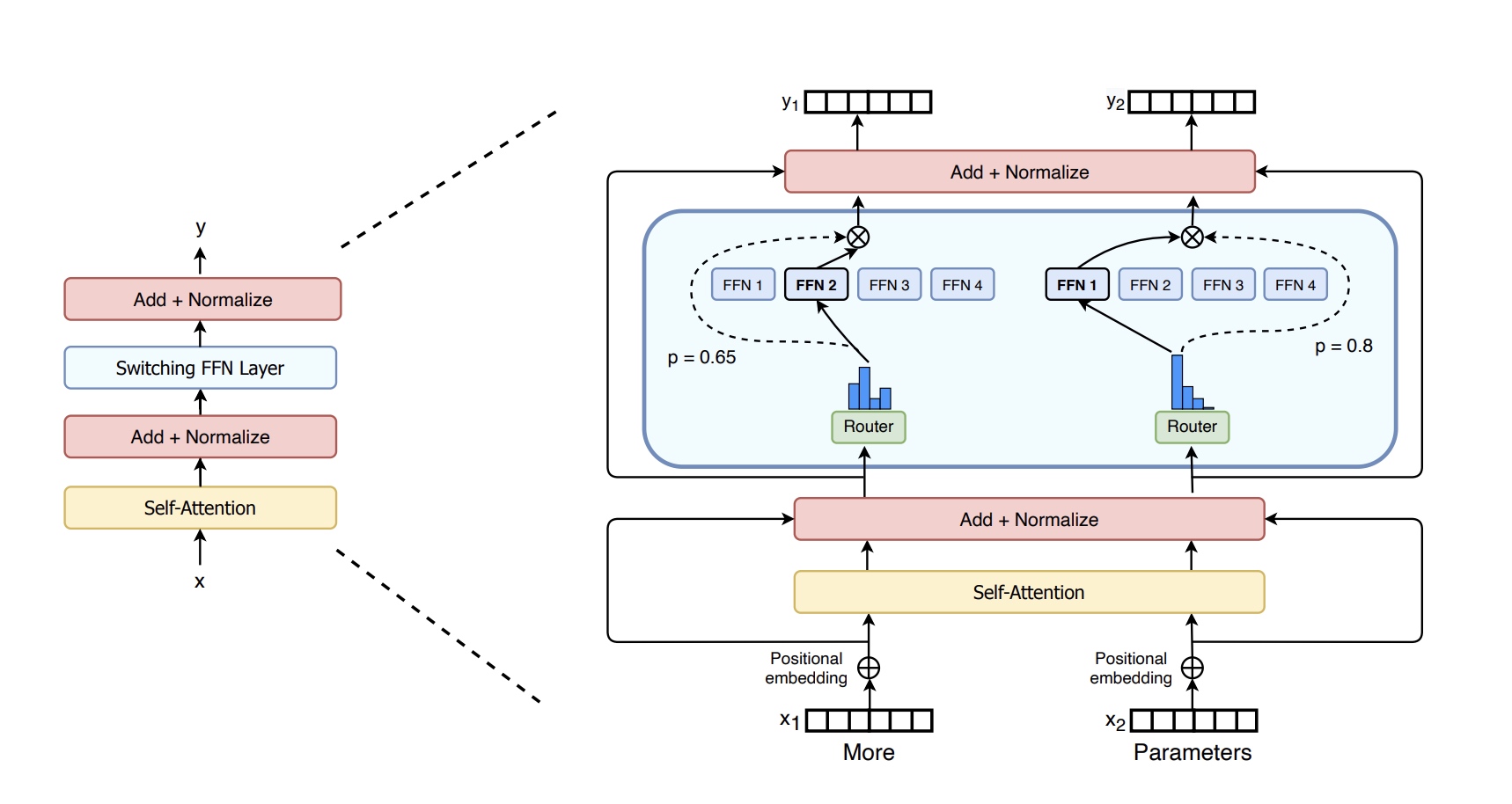
Switch Transformers中使用稀疏FFN层(图中蓝色框部分)替换原有transformer中的稠密FFN层. 稀疏FFN层对于输入token的处理是相互独立的, 上图中输入有两个token分别是More和Parameters, 每个token都会被随机路由到4个expert中的1个(实线), 输出会把选择上FFN层的输出乘上门控权重(虚线).

1.1 简化稀疏路由

回顾下之前的MoE层的门控方法, 网络接收一个输入token(x), 输出会路由到top-K个专家进行计算. 选择专家的过程如下, \(W_r\) 是门控的权重, \(p_i(x)\) 是专家i对输入x门控输出值, \(\mathcal{T}\) 是top-K个专家的下标集合.

\[\begin{gather} h(x)=W_r \cdot x \\ p_i(x) = SoftMax(h(x_i)) = \frac{e^{h(x)_i}}{\sum_j^N e^{h(x)_j}} \\ y = \sum_{i \in \mathcal{T}} p_i(x)E_i(x) \end{gather}\]

Switch Transformers中的Switch Layer对于这里的门控选择进行了优化, 从top-K个专家改为1个专家, 好处有三点:(1)由于只有一个专家, 对应的门控计算量节省 (2)专家对应的容量减半, 每个token只会路由到一个专家 (3)路由简化后对应的通信代价也下降了.

下面解释下专家使用不同的专家容量系数的情况, 名词解释如下:

  • 专家: 分布在不同的device上, 每个专家是一个FFN网络, 有独立的权重
  • 专家容量: 每个专家处理的batch大小, 公式为(tokens_per_batch/num_experts)*capacity_factor
  • 容量系数: 计算专家容量时乘上系数, 可以为专家多分配一些buffer来改善token溢出的情况

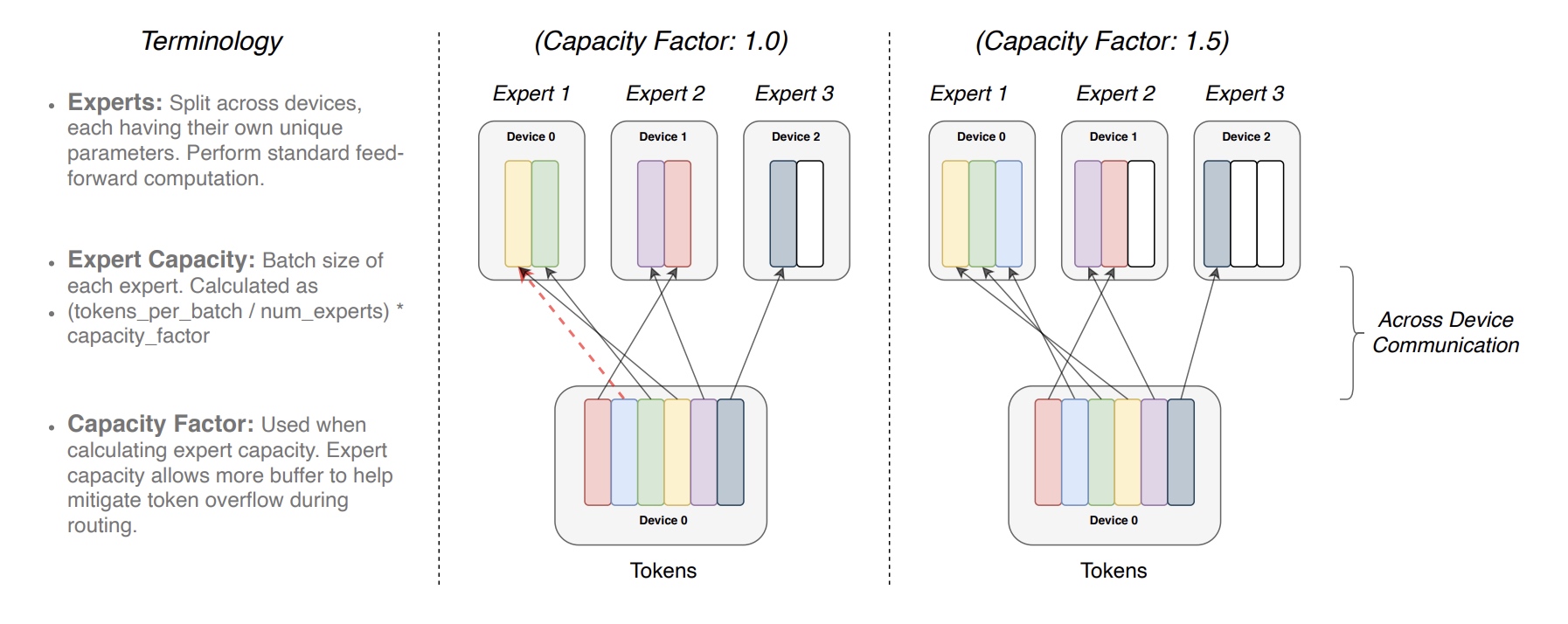每个专家有固定的专家容量((total_tokens/num_experts) x capacity_factor), 上图capacity_factor为1的时候, 每个device能处理的token个数为2, device0处理的token已经满了, 这时有新的token来的话就会溢出; 当capacity_factor为1.5的时候, 每个device可以处理3个token, 这时就没有token溢出了.

1.2 高效稀疏路由

1.2.1 分布式路由实现(Distributed Switch Implementation)

一个重要的点在于专家容量系数的设置, 如果专家容量系数设置过小, 太多的token被路由到一个专家上, 会造成溢出的token走了残差分支直接传给下一层; 如果专家容量系数设置过大, 会造成memory和计算的浪费. 专家容量定义如下:

\[\begin{gather} expert\ capacity=(\frac{token\ per\ batch}{number\ of\ experts}) \times capacity\ factor \end{gather}\]

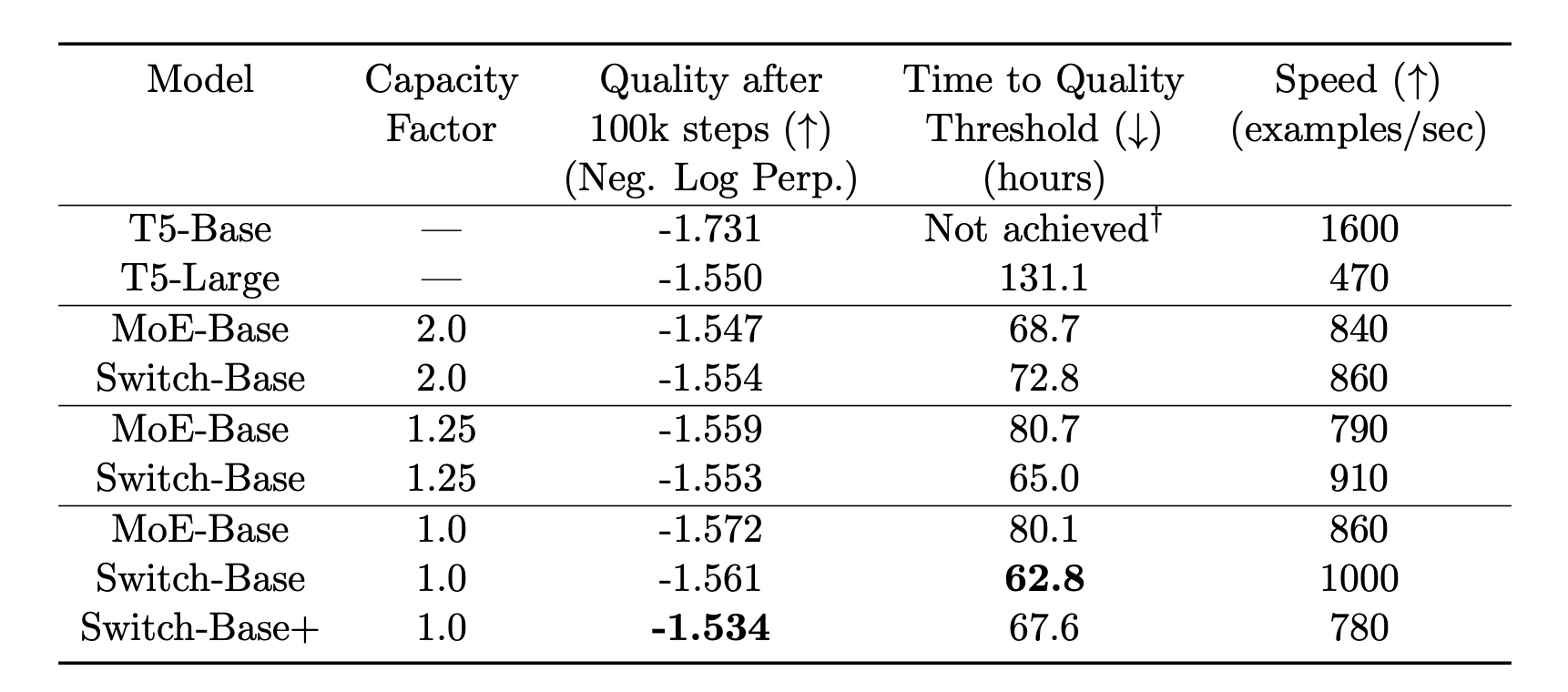
这里比较了不同容量系数对效果的影响, 效果质量采用了negative log perplexity进行衡量, 所有MoE采用了相同的128个专家.

1.2.2 可微分的负载均衡的损失函数 (A Differentiable Load Balancing Loss.)

对于Switch Layer来说, 辅助损失会被加到总的损失上. 给定 \(i\) 从1到N的 \(N\) 个专家, 一个batch \(\mathcal{B}\) 中有 \(T\) 个token, 损失计算公式如下:

\[\begin{gather} loss = \alpha \cdot N \cdot \sum^N_{i=1} f_i \cdot P_i \\ f_i = \frac{1}{T} \sum_{x \in \mathcal{B}} \mathbb{1}\{\mathnormal{argmax}\ p(x) = i\} \\ P_i = \frac{1}{T} \sum_{x \in \mathcal{B}} p_i(x) \end{gather}\]

\(f_i\) 分配给专家 \(i\) 的token数的比例, \(P_i\) 是分配给专家 \(i\) 的门控比例; \(P\)是可微的, 但 \(f\) 是不可微的; 在均匀路由的情况下，每个专家模型被选择的概率是 (\(\frac{1}{N}\)), 为了保持损失函数在不同数量的专家模型下的一致性，最终的损失会乘以专家模型的数量 (\(N\)), 对于公式表示为 \(\sum^N_{i=1}(f_i \cdot P_i) = \sum^N_{i=1} (\frac{1}{N} \cdot \frac{1}{N}) = \frac{1}{N}\).

最终超参数 \(\alpha\) 这里设置为 \(\alpha = 10^{-2}\), 是因为这个值足够大，可以有效地确保负载均衡; 同时，这个 ( ) 值又足够小，不会对主要的交叉熵损失函数（primary cross-entropy objective）产生过大的干扰。交叉熵损失函数通常是分类问题中的主要目标函数，用于衡量模型预测的准确性。\(\alpha\) 范围为 \(10^{-1} \sim 10^{-5}\).

1.3 预训练与微调训练优化

  • 大稀疏模型训练应用选择性精度: 选择性精度（Selective Precision）是一种技术，用于在计算资源和性能之间找到最佳平衡, 是指在计算过程中根据需要对不同部分的数据或计算使用不同的数值精度, 这里对应指的bfloat16. 在Switch Transformers训练过程中使用bfloat16训练, 把路由输入类型转为float32类型, float32只用在路由函数计算内部, 对于路由的输出又被转为bfloat16, 最终收益如下, 效果与效率达到了最好的情况.

  • 选择较小的参数初始化: 这里通过截断正态分布(truncated normal distribution)来进行权重初始化, 对应均值\(\mu=0\), 标准差 \(\sigma=\sqrt{s/n}\), s是缩放超参数(当前为0.1), n是权重矩阵的输入单元的个数(例如fan-in连接到该神经元的前一层神经元的数量). 截断正态分布生成的值会在\(([ \mu - 2\sigma, \mu + 2\sigma ])\)之外被截断，即任何超出这个范围的值会被重新抽取，直到它们落在这个范围内。如下图中小一点的缩放系数s=0.1效果比s=1更好.

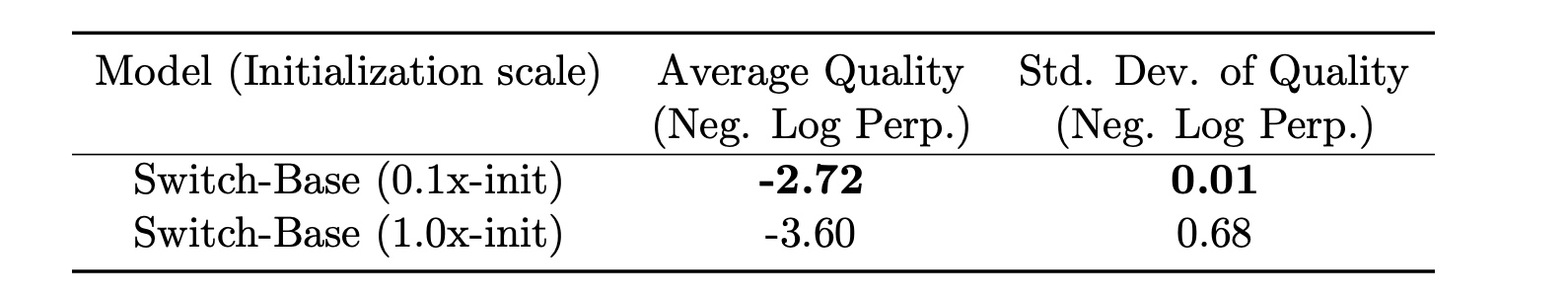
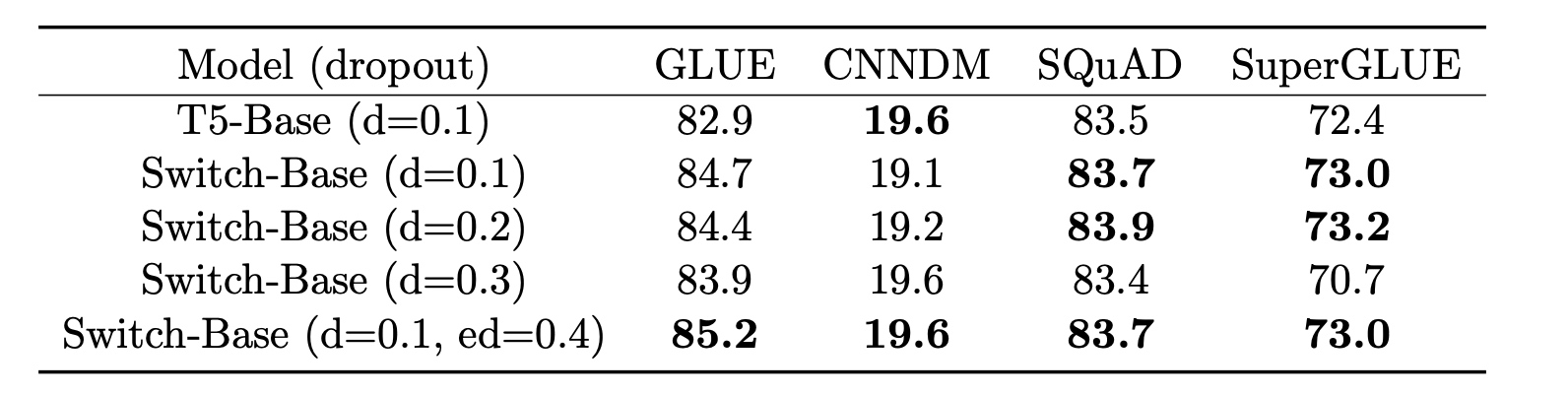
  • 模型正则化: 这里在expert中加入dropout, 被称为\(expert\ dropout\), 只在前向计算中加入dropout, 从下图中可以看出来对训练效果的影响. 对于非moe层设0.1的dropout, 对于expert设0.4的dropout, 提升了4个下游任务的指标.

2. DP/MP/EP并行设计(Designing Models with Data, Model, and Expert-Parallelism)

随意增加专家数量会面对收益递减的现象是一个实际问题。为了解决这一问题，可以采用一些互补的扩展策略. 常见的策略是同步增大transformer中的参数, 像 \(d_{model}\) 和 \(d_{ff}\), \(d_model\) 是输入和输出的词嵌入向量维度, \(d_ff\) 是前馈神经网络FFN中的隐藏层维度. 增大后显存超过单机情况后, 就要考虑使用 \(SPMD\) 多机并行了, 这节讨论了数据并行/模型并行/专家并行的使用.

2.1 回顾前馈神经网络FFN层

假设batch中有 \(\mathcal{B}\) 个token, 每个token的embedding维度是 \(d_{model}\). FFN层输入输出的shape都是 \([B, d_{model}]\), 中间产出 \(h\) 的shape是 \([B, d_{ff}]\), \(d_{ff}\) 比 \(d_{model}\) 要大, 比如4倍关系. 中间产出 \(h=xW_{in}\), 以及对应输出 \(y=ReLU(h)W_{out}\), \(W_{in}\) 与 \(W_{out}\) 的shape大小分别是 \([d_{model}, d_{ff}]\) 和 \([d_{ff}, d_{model}]\).

2.2 数据并行/模型并行/专家并行说明

接下来准备展示了如何对weight和batch data进行不同设备上的切分, 总的core个数为 \(N\), 数据并行的切片个数为 \(n\), 模型并行的切片个数为 \(m\), 总的切片个数等于总的core的个数, 即 \(N=n \times m\). 输入包含有 \(B\) 个Token的batch data 被n个数据并行core切分, 每个core上有 \(B/n\) 个token. 参数权重 \(d_{ff}\) 被m个模型并行core切分. 对于专家并行有 \(E\) 个专家, 每个专家的容量为 \(C\) 个token. 相关描述如下:

以下数据与权重并行的切分策略图, 4x4的虚线切分了16个块对应16个core的device. 第一行是模型权重的切分图, 不同颜色表示独立的参数权重, 相同颜色表示相同的权重. 第二行表示数据切分图, 不同颜色表示使用的token数据不同, 相同颜色表示相同的token数据.

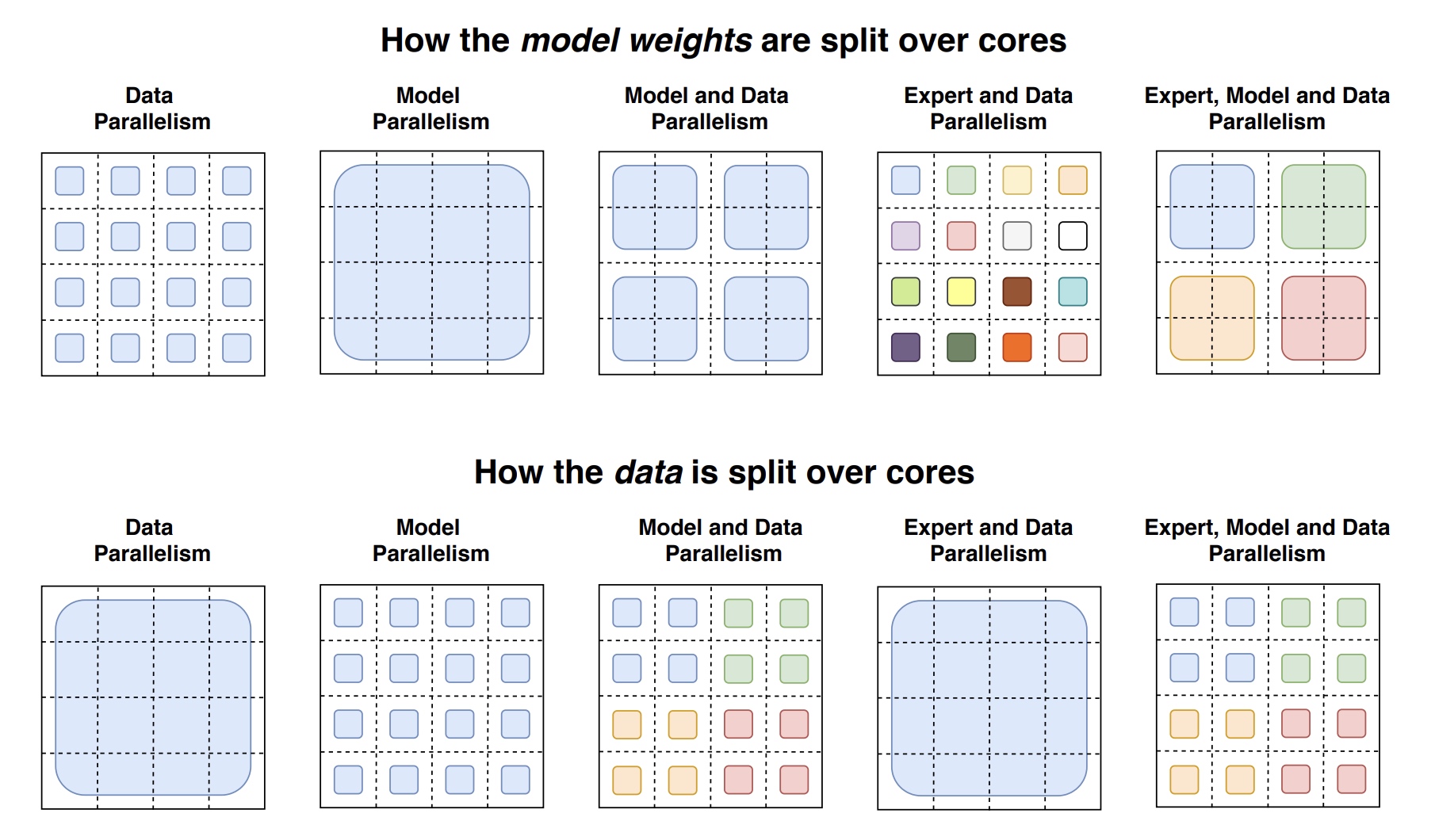
  • 数据并行: 在上图中第一列, 只有数据并行时 \(n=N, m=1\), 在前反向计算过程中没有通信, 只在优化器阶段进行所有core的同步, weight权重在所有core上进行复制一份, 数据是所有core计算时分别处理一部分.
  • 模型并行: 在上图中第二列, 只有模型并行时 \(n = 1, m = N\), weight权重被16个core切分为16块, 每个core上保留一部分; 在数据处理上, 每个core都会处理全量的 \(B\) 个token数据, 由于在 \(d_{ff}\) 维度上进行了模型切分, 计算FFN第二个矩阵乘法的结果时( \(ReLU(h)W_{out}\) ), 每个core都会去发送一个大小为 \([B, d_{model}]\) 的数据, 在每一个前向和反向过程中会调用的allreduce操作.
  • 数据并行/模型并行混合: 在上图中第三列, 每个core会分到 \(B/n\) 个token处理, 以及会分到 \(d_{ff}/m\) 的权重的大小与中间activation产出. 在前向和反向通信时的tensor大小 \([B/n, d_{model}]\). 这时cores会被划分为4组, 每一组core上有一份全量的模型权重, 4组模型权重做数据并行, 4组模型组内模型切分做模型并行; 数据切分在不同组模型处理数据不一样(用4种颜色区分), 在一个组内的4个core做模型并行, 数据会复制多份处理(例如一份蓝色数据复制成了多个小块)
  • 专家并行/数据并行混合: 专家并行时每个专家的权重都不一样, 互相独立, 所以模型权重颜色都不一样; 下方数据并行, 共同处理同一份数据, 也就是一个大的蓝色块, 跟第一列一样. 这里data切分的是按数据并行度 \(n\) 来进行的, 每个专家的输出shape大小是 \([n, B/n, E, C]\), 然后输出会跟输入tensor进行相乘 \(einsum([n, B/n, d_{model}], [n, B/n, E, C], dimension=[B/n])\), 得到结果大小为 \([n, E, C, d_{model}]\). 每个core都有各自的expert, 对结果( \([E, C, d_{model}]\) )进行alltoall操作, 从 \(n\) 维度切分变为 \(E\) 维度切分.
  • 专家并行/数据并行/模型并行: 从模型权重切分上, 与数据并行/模型并行混合一样, 区别在于expert专家权重各不相同, 所以有4个不同色块, 每个色块中4个core来进行模型切分; 下面数据切分上, 与数据并行/模型并行混合一样, 每组处理不同的数据. 为了最优的模型设计, 寻求FLOPS与模型参数的平衡, 增大专家数能增大参数量, 但FLOPS没有增长. 为了增加FLOPS, 我们增大了 \(d_{ff}\) 的大小, 对应模型并行度 \(m\) 也会增大, 由于 \(N=n \times m\) 是个定值, 所以 \(n\) 会对应减少.

2.3 万亿模型设计(Towards Trillion Parameter Models)

设计了两个Switch Transformer模型, 分别是395 billion(3950亿)和1.6 trillion(1.6万亿)参数量, 其中 Switch-C 只用了专家并行, 没有用模型并行.

3. 参考