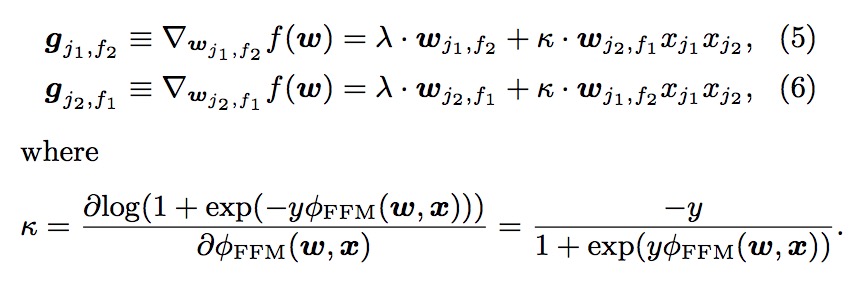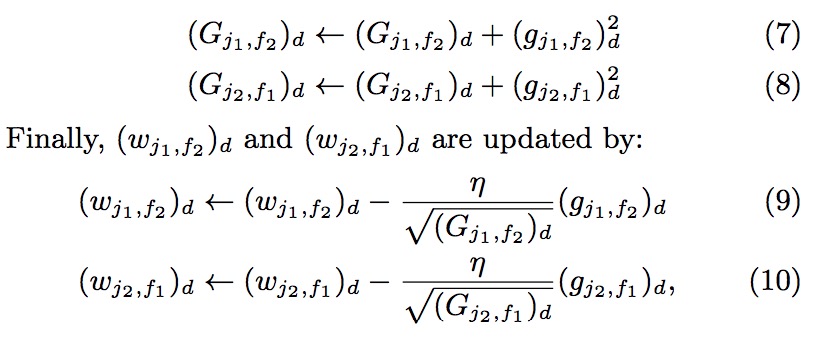FM(Factorization Machines)、FFM(Field-aware Factorization Machines)算法介绍
高维稀疏场景描述
机器学习中一个通常的预估任务是为了预估一个函数$ y: ^n \(, 预估过程中使用一组具有实数值的特征向量\) ^n $ 去预测目标 $ \((在回归预估中\) = $, 在分类预估中 $ = +, - \(). 高维稀疏场景下向量\) \(中大部分元素\) x_i \(的值都是0, 我们定义\) m(x) $为向量 $ $ 中非零元素的个数,$ _{D} \(为所有向量\) \(的\) m(x) \(值的平均值。实际中(例如推荐系统)经常会碰到超大规模稀疏的情况(\) _{D} n \()。 下面举一个例子,假设我们有一个电影的推荐系统,系统中每一条记录表示一个用户(\) u U \()在某个时间点(\) t \(}对一个电影(item)(\) i I \()的评分(\) r , 2, 3, 4, 5 \(). 用户\) U $和电影item $ I $的示例如下: > $ U = Alice(A), Bob(B), Charlie(C), $ > $ I = Titanic (TI), Notting Hill (NH), Star Wars (SW), Star Trek (ST), $ 系统可观测到的用户数据为$ S $示例如下: > $ S = (A, TI, 2010-1, 5), (A, NH, 2010-2, 3), (A, SW, 2010-4, 1), $ > $ (B, SW, 2009-5, 4), (B, ST, 2009-8, 5), (C, TI, 2009-9, 1), (C, SW, 2009-12, 5) $
如下图所示: 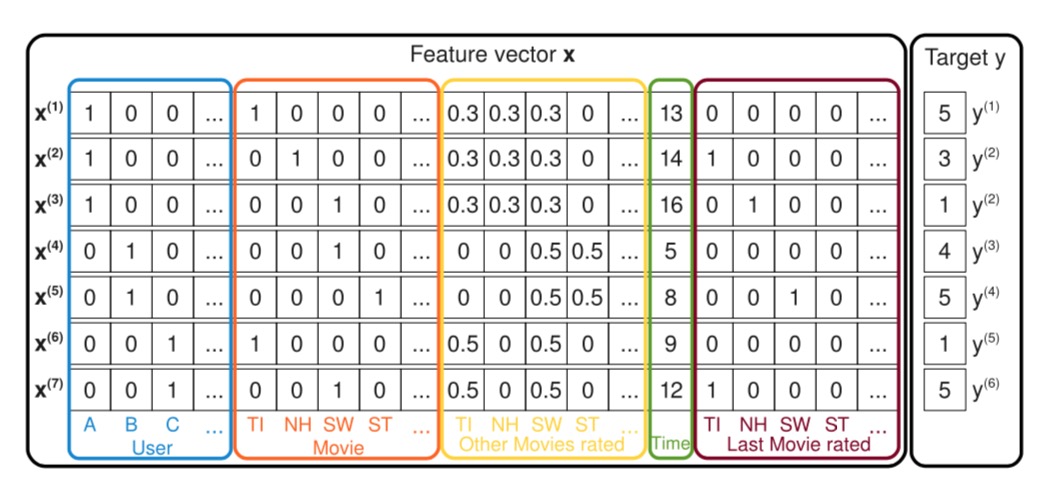
图中展示了如何从观测到的用户数据$ S \(去创建训练所需要的特征向量的过程,图中蓝色框住的地方表示系统中的用户,每一条记录都表示一个用户的一个行为对\) (u, i, t, r) S \(,上面\) S \(中的第一条记录\) (A, TI, 2010-1, 5) \(,Alice简写为A,在蓝框中\) (x_{A}^{(1)} = 1) \(,红色框表示看的电影的item,这里\) x_{TI}^{(1)} = 1 $. 黄色框中表示用户对历史看过的所有的电影的历史评分,这里历史评分的取值经过了归一化操作,归一化以后的值的和为1。绿色表示从09年1月开始计算经历的月份数。深红色的框表示用户上次评价的电影名, 评价过的电影对应的位置设置成1,未评价的设置成0。
Factorization Machines(FM)算法优点
参考Steffen
Rendle的论文
Factorization Machines(FM)算法过程
模型等式(Model Equation)
首先定义度为2的因子分解机的模型等式如下,这里度的含义是等式里采用了2维的交叉变量(interactions between variables)作为特征,即公式中的$ x_i x_j $。 > $ () := w_0 + _{i=1}^n w_{i} x_{i} + _{i=1}^{n} _{j=i+1}^{n} _{i} _{j} x_i x_j $ (一)
其中公式中$ w_0 , ^{n}, ^{n k} $, $ , $ 表示两个大小为k的向量的点乘。即: > $ _{i}, _{j} := _{f=1}^{k} v_{i,f} v_{j,f} $
$ v_{i} $ 表示用 $ k $ 个因子来表示第 $ i $个变量, 这里 $ k _0^{+} $ 是一个超参数, 用来定义因子分解的维数。2-way(即度为2)的FM算法中用到了所有的单一变量,以及任意两个变量的交叉变量(interaction)。$ w_{0} $ 是全局的bias值,$ w_{i} $ 表示第 $ i $ 个变量的权重,$ _{i,j} := _i _{j} $ 表示第 $ i $ 个变量和第 $ j $ 个变量的交叉(interaction)变量,不像其他算法中使用 $ w_{i,j} $ 来表示每一个交叉变量的权重,FM采用因式分解的方式来表示。
FM模型的表达能力(Expressiveness)
对于每一个正定矩阵$ $ 都存在一个矩阵 $ $,使得 $ = ^t $。对于前面说到的k值如果足够的大的话,FM算法可以表达整个矩阵 $ $,然而在稀疏矩阵中k值应该选的小一些,因为没有足够的数据来计算,通过限制k的大小,可以使得FM算法在高维稀疏的情况下表达能力会更好。
稀疏场景下的参数估计
电影场景下,特征的稀疏经常会碰到没有足够的数据来电影和人之间的喜好程度,但是FM通过因子分解的方法来解决这个问题,比如我们要去评估人Alice(A)对电影Star Trek(ST)的评分(Rating),但观察到的电影数据中,没有发现一条记录中 $ x_A $ 和 $ x_{ST} $ 都不为0,即历史纪录中人A与电影ST没有过任何交集( $ w_{A, ST} = 0 $ ), 但是通过 $ _A _{ST} $ 就可以估计这种情况。
模型计算
直接计算公式(一)的时候两两变量的交叉都要计算,所以公式(一)的时间复杂度为$ O(kn^2) $, 但是我们可以通过变换使得在线性时间 $ O(kn) $ 的时间复杂度下计算完。具体推导如下:
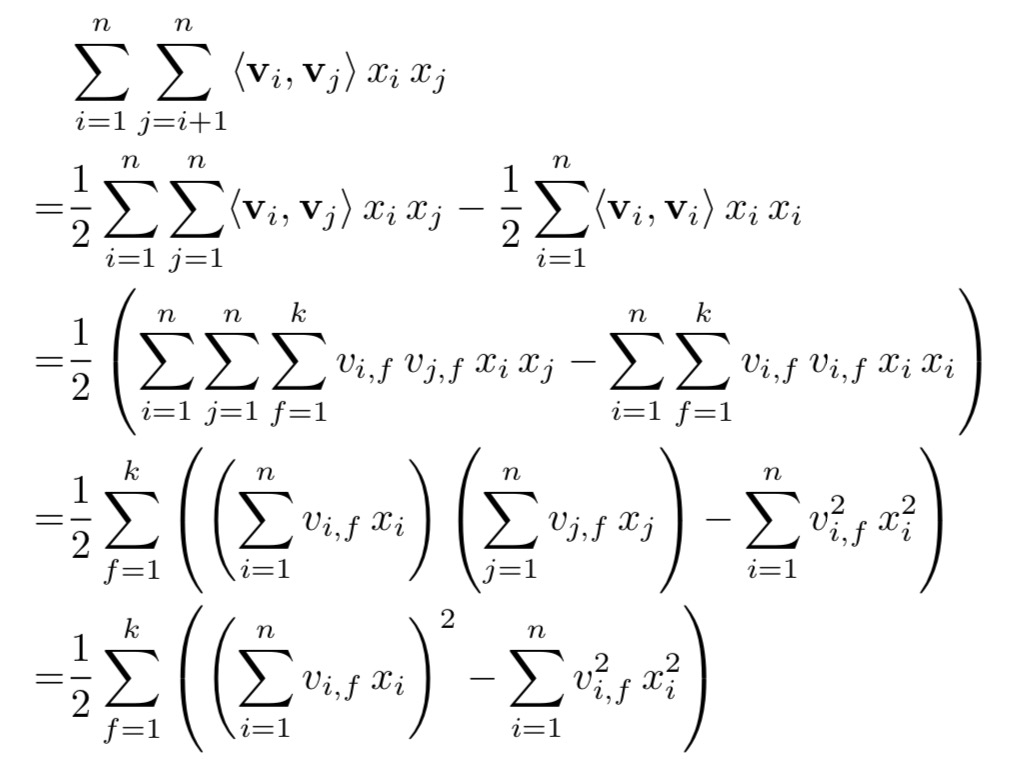
最后的等式中线性复杂度只依赖k和n两个变量, 可以在 $ O(kn) $ 的时间复杂度下计算完成。对于稀疏情况下,只用计算不为0的元素即可。
FM的使用场景
FM的使用场景可以用在以下几个方面: * 回归: 采用最小平方误差,$ () $ 的结果可以用来回归 * 二分类: 采用hinge loss或者logit loss, 可以通过$ () \(的正负来作为二分类的依据 * 排序: 可以根据\) () $ 值的大小来对向量 $ $ 进行排序
FM训练计算过程
使用梯度下降法来进行参数的更新,FM算法中的梯度计算如下: 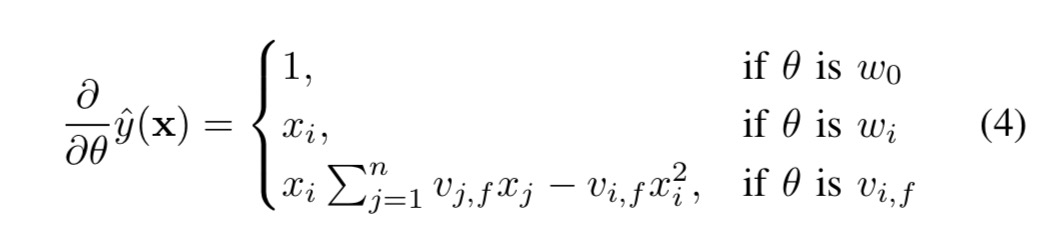
公式中$ _{j=1}^{n} v_{j,f} x_{j} $ 是跟 $ i $ 相互独立的,所以这里可以被提前计算出来(例如可以在计算 $ (x) $ 的时候顺便计算)。通常来说gradient计算都可以在常数时间( $ O(1) $ )内计算出来,参数的更新可以在 $ O(kn) $ 时间内计算出来。
FFM(Field-aware Factorization Machines)算法
FFM算法简介
FFM算法是基于FM算法而来,从CTR预估谈起,最初的优化问题为 > $ _{w} || ||_{2}^{2} + _{i=1} ^{m} log(1 + exp(-y_{i} _{LM}(, _i))) $
这里$ $ 是正则化参数, 损失函数中我们考虑使用线性模型(Linear Model, 简写LM): $ _{LM}(, ) = $
进一步优化我们发现,通过度为2的多项式特征组合可以更好的获取特征信息,所以Poly2算法在线性算法的基础上增加了特征的两两组合,即: > $ _{Poly2}(, ) = _{j_{1}=1}^{n} _{j_{2}=j+1}^{n} w_{h(j_{1}, j_{2})} x_{j_1} x_{j_2} $
这里$ h(j_{1}, j_{2}) $ 将 $ j_{1}, j_{2} $ 编码成为一个自然数的编号,时间复杂度为$ O(^{2}) $,这里 $ $ 表示每一条样本中非零元素个数的平均值。
然后FM的改动如第一大节描述的那样,对每一个特征增加了一个隐式向量(latent vector),然后交叉特征的权重用各自两个特征对应的隐式向量的成绩来表示,即用$ (_{j_1} _{j_2}) $ 来替换之前的 $ w_{h(j_{1}, j_{2})} $, 具体公式如下: >优化以后有 $ _{FM}(, ) = _{j=1}^{n}( - _{j} x_{j}) _{j} x_{j} $ 这里 $ = _{j'=1}^{n} _{j'} x_{j'} $
时间复杂度为$ O( k) $
FFM算法在之前基础上增加了域(Field)的概念,比如人的特征有年龄,性别等,虽然是不同特征,但是都归结为"人"的这个域下面,电影的特征有电影名,上映时间等,也都可以归结为"电影"这个域下面。每个特征都有对应的编号,同理也可以给域增加编号,编号以后在FM的算法基础上,原来FM算法中每个特征对应的那一个隐式向量,在FFM算法中扩展成为每个特征在每个域下面都各有一个隐式向量,例如原来特征"年龄"对应的$ _{年龄} $ 就扩展为了 $ _{年龄, 人} $ 和 $ _{年龄, 电影} $ 两个向量,扩展的向量的个数等同于域的个数,即在每个域下面每个特征都各有一个隐式向量。由此FFM算法的公式可以定义为下面这个式子: >FFM算法求解过程
FFM算法使用随机梯度下降(SG)的方法进行求解,采用AdaGrad的方式来进行参数的更新。
求解过程跟FM非常相似,这里不在赘述,附上求解的过程如下: