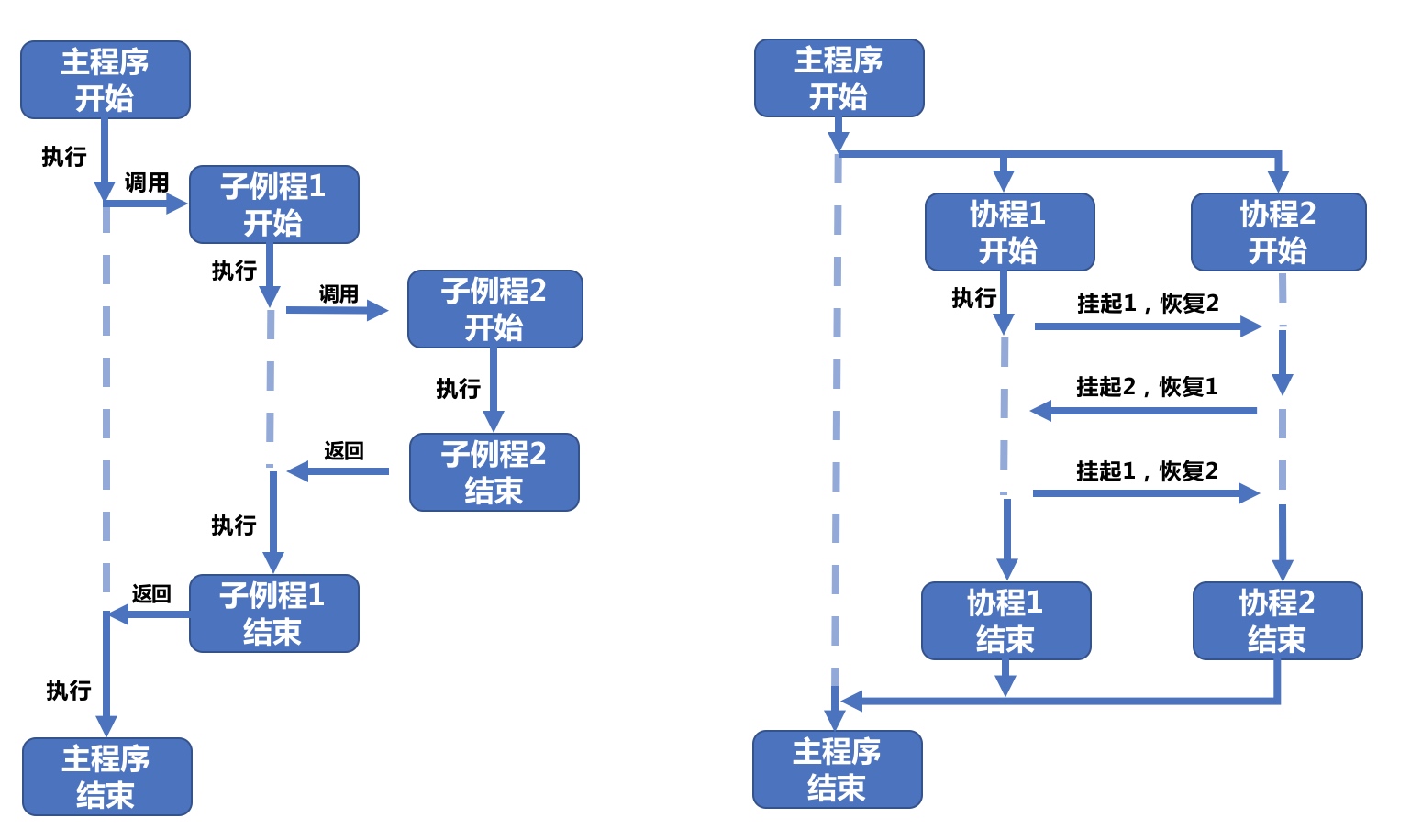
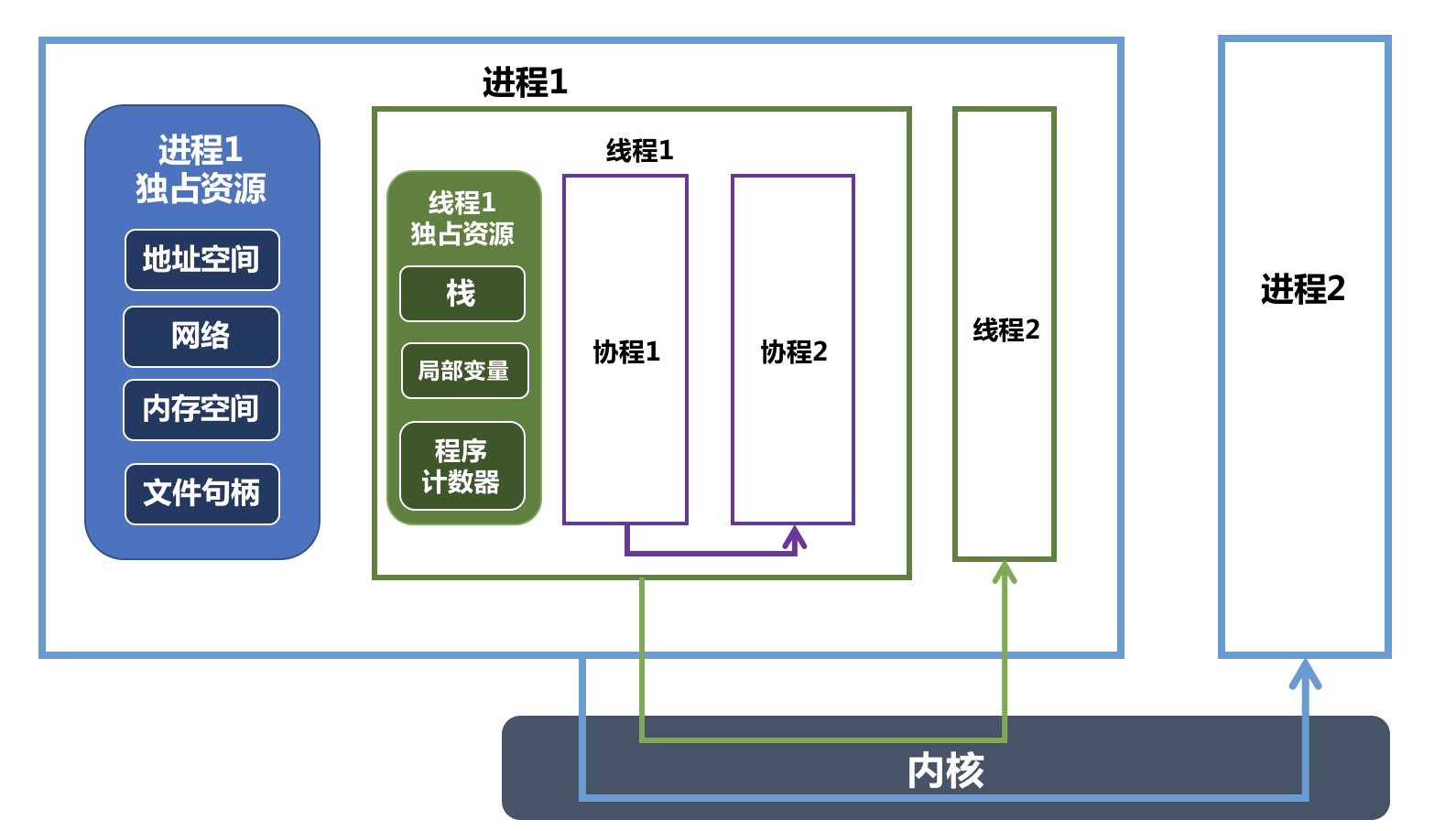
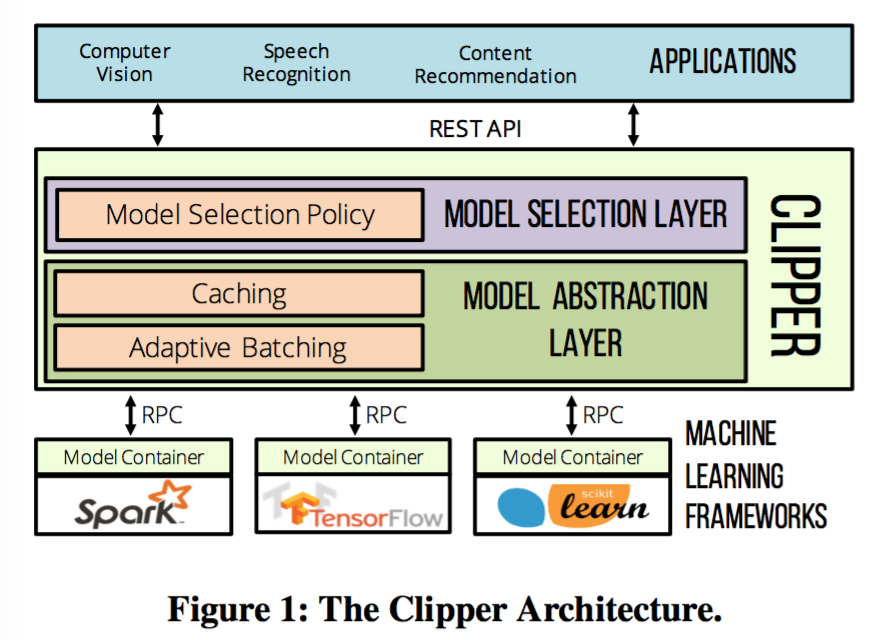
高维稀疏场景描述
机器学习中一个通常的预估任务是为了预估一个函数$ y: ^n \(, 预估过程中使用一组具有实数值的特征向量\)
^n $ 去预测目标 $ \((在回归预估中\) =
$, 在分类预估中 $ = +, - \().
高维稀疏场景下向量\) \(中大部分元素\) x_i \(的值都是0, 我们定义\) m(x) $为向量 $ $
中非零元素的个数,$ _{D} \(为所有向量\)
\(的\) m(x) \(值的平均值。实际中(例如推荐系统)经常会碰到超大规模稀疏的情况(\)
_{D} n \()。
下面举一个例子,假设我们有一个电影的推荐系统,系统中每一条记录表示一个用户(\)
u U \()在某个时间点(\) t \(}对一个电影(item)(\) i I \()的评分(\) r , 2, 3, 4, 5 \(). 用户\) U $和电影item $ I $的示例如下:
> $ U = Alice(A), Bob(B), Charlie(C), $ > $ I = Titanic (TI),
Notting Hill (NH), Star Wars (SW), Star Trek (ST), $
系统可观测到的用户数据为$ S $示例如下: > $ S = (A, TI, 2010-1, 5),
(A, NH, 2010-2, 3), (A, SW, 2010-4, 1), $ > $ (B, SW, 2009-5, 4), (B,
ST, 2009-8, 5), (C, TI, 2009-9, 1), (C, SW, 2009-12, 5) $
如下图所示: 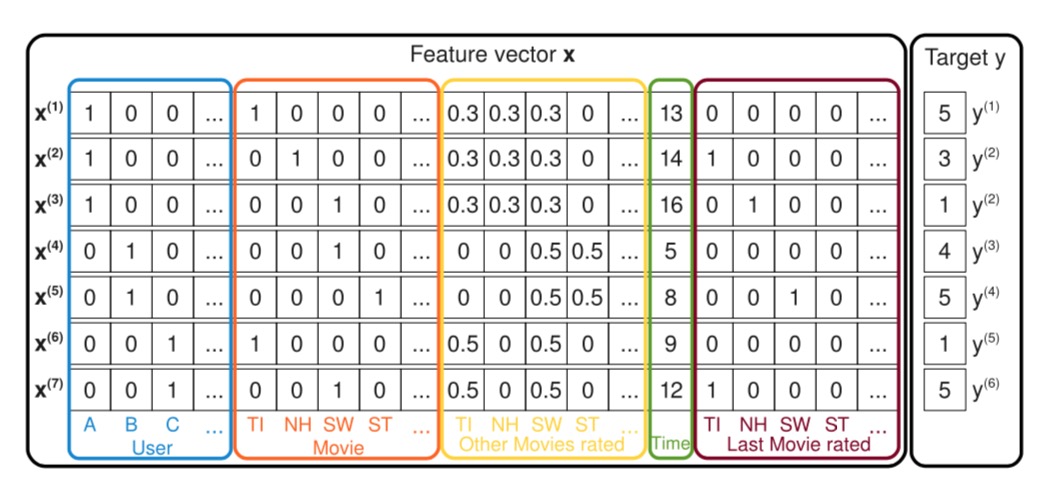
图中展示了如何从观测到的用户数据$ S \(去创建训练所需要的特征向量的过程,图中蓝色框住的地方表示系统中的用户,每一条记录都表示一个用户的一个行为对\)
(u, i, t, r) S \(,上面\) S \(中的第一条记录\) (A, TI, 2010-1, 5) \(,Alice简写为A,在蓝框中\) (x_{A}^{(1)} =
1) \(,红色框表示看的电影的item,这里\)
x_{TI}^{(1)} = 1 $.
黄色框中表示用户对历史看过的所有的电影的历史评分,这里历史评分的取值经过了归一化操作,归一化以后的值的和为1。绿色表示从09年1月开始计算经历的月份数。深红色的框表示用户上次评价的电影名,
评价过的电影对应的位置设置成1,未评价的设置成0。
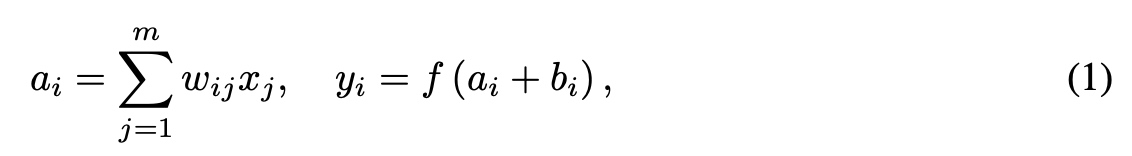
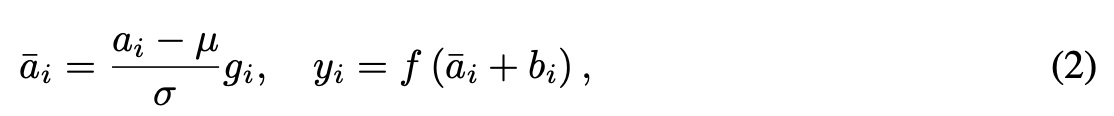
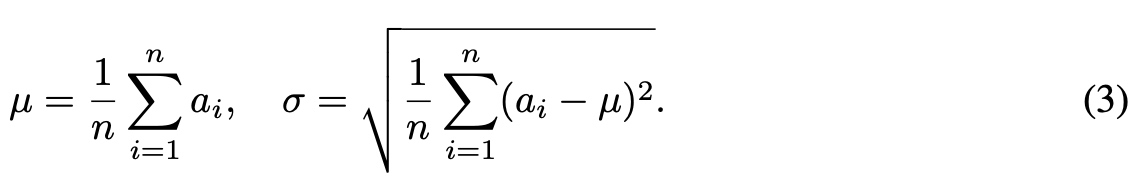
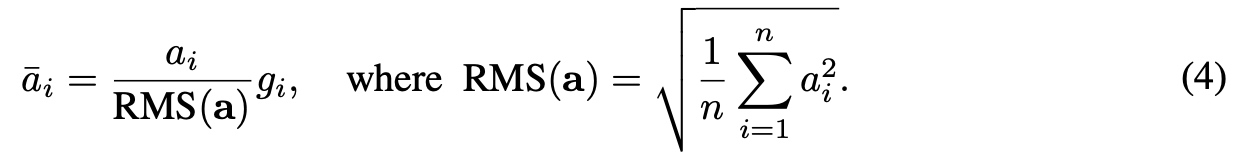 RMS中去除了
RMS中去除了